Abstract
This paper investigates the amplitude jump and tooth surface impact characteristics of straight bevel gear systems with backlash. Using the harmonic balance method, a comprehensive dynamic model of the gear system is established. The Broyden quasi-Newton method and pseudo-arc-length continuation algorithm are employed to obtain the parameter solution domain boundary structures in the parameter planes constructed by frequency, backlash, time-varying stiffness, static transmission error, and load. The sensitivity of amplitude jumping, multi-valued solutions, and meshing impacts to the parameters is explored. The results reveal complex dynamic behaviors, especially at the meshing frequency, with amplitude jumping and multi-valued solutions observed in the main resonance regions. The tooth surface impact phenomenon is severe at small backlashes but stabilizes when the backlash exceeds a critical value. The system’s dynamic characteristics are insensitive to time-varying meshing stiffness but sensitive to high-speed light loads and large tooth surface errors. The proposed parameter solution domain boundary structures provide valuable data support for the structural design of bevel gears.
Keywords: straight bevel gear system, dynamic characteristics, harmonic balance method, parameter solution domain boundary, amplitude jump, tooth surface impact
1. Introduction
Straight bevel gears are widely used in automotive, aerospace, and industrial machinery due to their compact structure and high transmission efficiency. However, gear systems often exhibit nonlinear dynamic behaviors, such as amplitude jumping, multi-valued solutions, and tooth surface impacts, particularly in the presence of backlash and time-varying stiffness. These nonlinear phenomena can significantly affect the gear’s performance, lifespan, and noise levels. Therefore, a thorough understanding of the dynamic characteristics of straight bevel gear systems is crucial for their optimal design.
This paper aims to analyze the dynamic behaviors of straight bevel gear systems and establish parameter solution domain boundary structures in various parameter planes. By doing so, we provide a comprehensive data support for the structural design of bevel gears to ensure optimal performance and reliability.
2. Literature Review
Previous studies have extensively investigated the nonlinear dynamic behaviors of gear systems. Zhu et al. [1] analyzed the nonlinear frequency response of compound planetary gear systems. Ghosh et al. [2] studied the stability of a six-degree-of-freedom torsional-translational gear pair with friction. Zhang et al. [3] addressed the random vibration problem in two-stage gear transmission systems. In the context of bevel gears, Wang et al. [4] established a dynamic model of a bevel gear system with backlash and bearing support, analyzing its bifurcation and amplitude jump characteristics. Hua et al. [5] studied the influence of bearing support stiffness on the dynamic meshing force of a bevel gear rotor system.
While these studies have contributed significantly to our understanding of gear dynamics, there is still a lack of comprehensive analysis of parameter solution domain boundary structures, especially for straight bevel gear systems. This gap motivates the present work.
3. Dynamic Model of the Straight Bevel Gear System
3.1 System Description
The straight bevel gear system considered in this study consists of two meshing gears supported by elastic bearings. A schematic diagram of the system. The gears are assumed to be rigid bodies with point masses located at their centers of mass. The bearings are modeled as linear spring-damper systems.
3.2 Governing Equations
The dynamics of the system are governed by the following equations of motion:
m1x¨1+cx1x˙1+kx1x1m1y¨1+cy1y˙1+ky1y1m1z¨1+cz1z˙1+kz1z1J1θ¨1m2x¨2+cx2x˙2+kx2x2m2y¨2+cy2y˙2+ky2y2m2z¨2+cz2z˙2+kz2z2J2θ¨2=Fx1=Fy1=Fz1=T1−r1Fz1=−Fx2=−Fy2=−Fz2=−T2+r2Fz2
where m1 and m2 are the masses of the gears, cij and kij are the damping and stiffness coefficients of the bearings, J1 and J2 are the moments of inertia of the gears, r1 and r2 are the base circle radii, T1 and T2 are the driving and resisting torques, respectively, and Fxi, Fyi, and Fzi (i = 1, 2 \)) are the components of the meshing force in the \( x, y, and z directions, respectively.
The meshing force Fn along the line of action is given by:
Fn=kh(t)f(Λn)+chΛ˙n
where kh(t) is the time-varying meshing stiffness, ch is the meshing damping coefficient, Λn is the relative displacement along the line of action, and f(Λn) is the backlash function defined as:
f(\Lambda_n) = begin{cases} Lambda_n – b_h, & \text{if } \Lambda_n > b_h \\ 0, & \text{if } |\Lambda_n| \leq b_h \\ Lambda_n + b_h, & \text{if } \Lambda_n < -b_h end{cases}
where 2bh is the backlash width.
3.3 Harmonic Balance Method
The harmonic balance method is employed to solve the nonlinear equations of motion. The solution is assumed to be periodic and can be expressed as a Fourier series:
x(t)=x0+n=1∑N[ancos(nωt)+bnsin(nωt)]
where x(t) represents any of the displacement or rotation variables, ω is the angular frequency, N is the number of harmonics considered, and an and bn are the Fourier coefficients.
Substituting the Fourier series into the equations of motion and equating the coefficients of like harmonic terms, a set of algebraic equations is obtained, which can be solved using numerical methods.
4. Parameter Solution Domain Boundary Structures
4.1 Parameter Planes
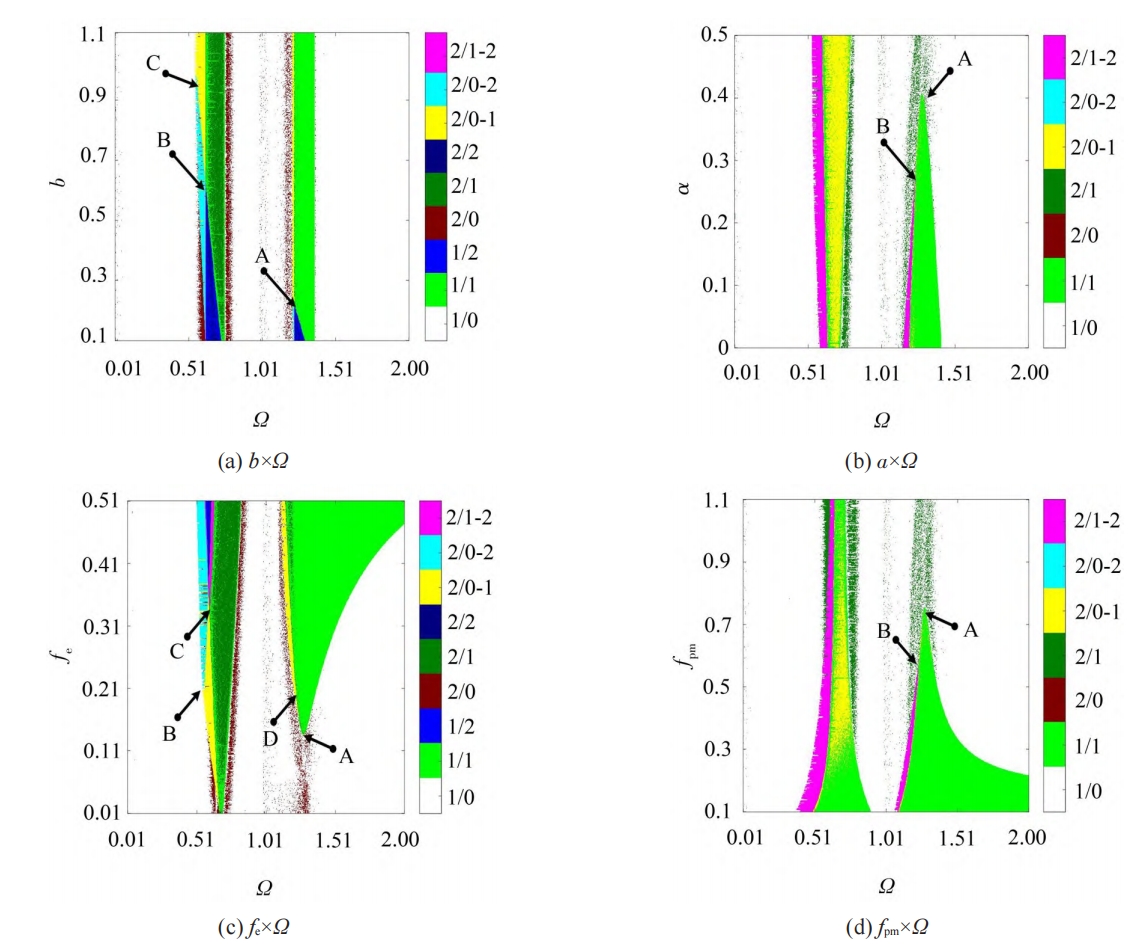
To investigate the sensitivity of the system’s dynamic characteristics to various parameters, parameter planes are constructed using frequency Ω, backlash bh, time-varying stiffness amplitude coefficient α, static transmission error coefficient fe, and load coefficient fpm. The following parameter planes are considered:
- Ω×bh
- Ω×α
- Ω×fe
- Ω×fpm
4.2 Solution Procedure
The Broyden quasi-Newton method and pseudo-arc-length continuation algorithm are used to solve the nonlinear algebraic equations obtained from the harmonic balance method. The algorithm traces out the solution curves in the parameter planes, revealing regions of stability, instability, and bifurcation.
4.3 Results and Discussion
4.3.1 Ω×bh Plane
The solution domain boundary structure in the Ω×bh plane. The system exhibits complex dynamic behaviors, with amplitude jumping and multi-valued solutions observed in the main resonance regions. At small backlashes, severe tooth surface impacts are observed, but the system stabilizes when the backlash exceeds a critical value (approximately ( b_h > 0.98 )).
Table 1: Dynamic behaviors in the Ω×bh plane.
| Backlash (( b_h )) | Dynamic Behavior |
|---|---|
| bh<0.98 | Amplitude jumping, multi-valued solutions, severe tooth surface impacts |
| bh≥0.98 | Stable response, reduced tooth surface impacts |
4.3.2 Ω×α Plane
The solution domain in the Ω×α plane reveals that the system’s dynamic characteristics are insensitive to time-varying meshing stiffness amplitude (\alpha \)). However, at high values of \( \alpha, the amplitude jumping and tooth surface impacts are slightly reduced.
Table 2: Dynamic behaviors in the Ω×α plane.
| Time-varying stiffness amplitude (( \alpha )) | Dynamic Behavior |
|---|---|
| Low α | Amplitude jumping, multi-valued solutions |
| High α | Slightly reduced amplitude jumping and tooth surface impacts |
4.3.3 Ω×fe Plane
The solution domain in the Ω×fe plane shows that the system’s dynamic characteristics are sensitive to static transmission errors (( f_e )). At high error levels, amplitude jumping and tooth surface impacts are significantly enhanced.
Table 3: Dynamic behaviors in the Ω×fe plane.
| Static transmission error (( f_e )) | Dynamic Behavior |
|---|---|
| Low fe | Stable response, reduced impacts |
| High fe | Enhanced amplitude jumping, severe tooth surface impacts |
4.3.4 Ω×fpm Plane
The solution domain in the Ω×fpm plane indicates that the system’s response is sensitive to load levels. At high-speed light loads, the amplitude jumping and tooth surface impacts are more pronounced.
Table 4: Dynamic behaviors in the Ω×fpm plane.
| Load coefficient (( f_{pm} )) | Dynamic Behavior |
|---|---|
| High loads | Stable response, reduced impacts |
| Low loads (high-speed) | Enhanced amplitude jumping, severe tooth surface impacts |
5. Conclusion
This paper investigated the dynamic characteristics of straight bevel gear systems using the harmonic balance method. Parameter solution domain boundary structures were established in various parameter planes, revealing the sensitivity of the system’s response to backlash, time-varying stiffness, static transmission errors, and load levels. The results indicate that amplitude jumping and multi-valued solutions are observed in the main resonance regions, with severe tooth surface impacts at small backlashes. The system stabilizes when the backlash exceeds a critical value. The dynamic characteristics are insensitive to time-varying meshing stiffness but sensitive to high-speed light loads and large tooth surface errors. The proposed parameter solution domain boundary structures provide valuable data support for the structural design of bevel gears, ensuring optimal performance and reliability.
