Planetary gear systems serve as critical components in industrial reducers, where cyclic and impact loads frequently induce surface fatigue failures like pitting. This paper establishes a dynamic model to evaluate pitting severity in planetary gears under transient impact loads through theoretical derivations, numerical simulations, and experimental validation.
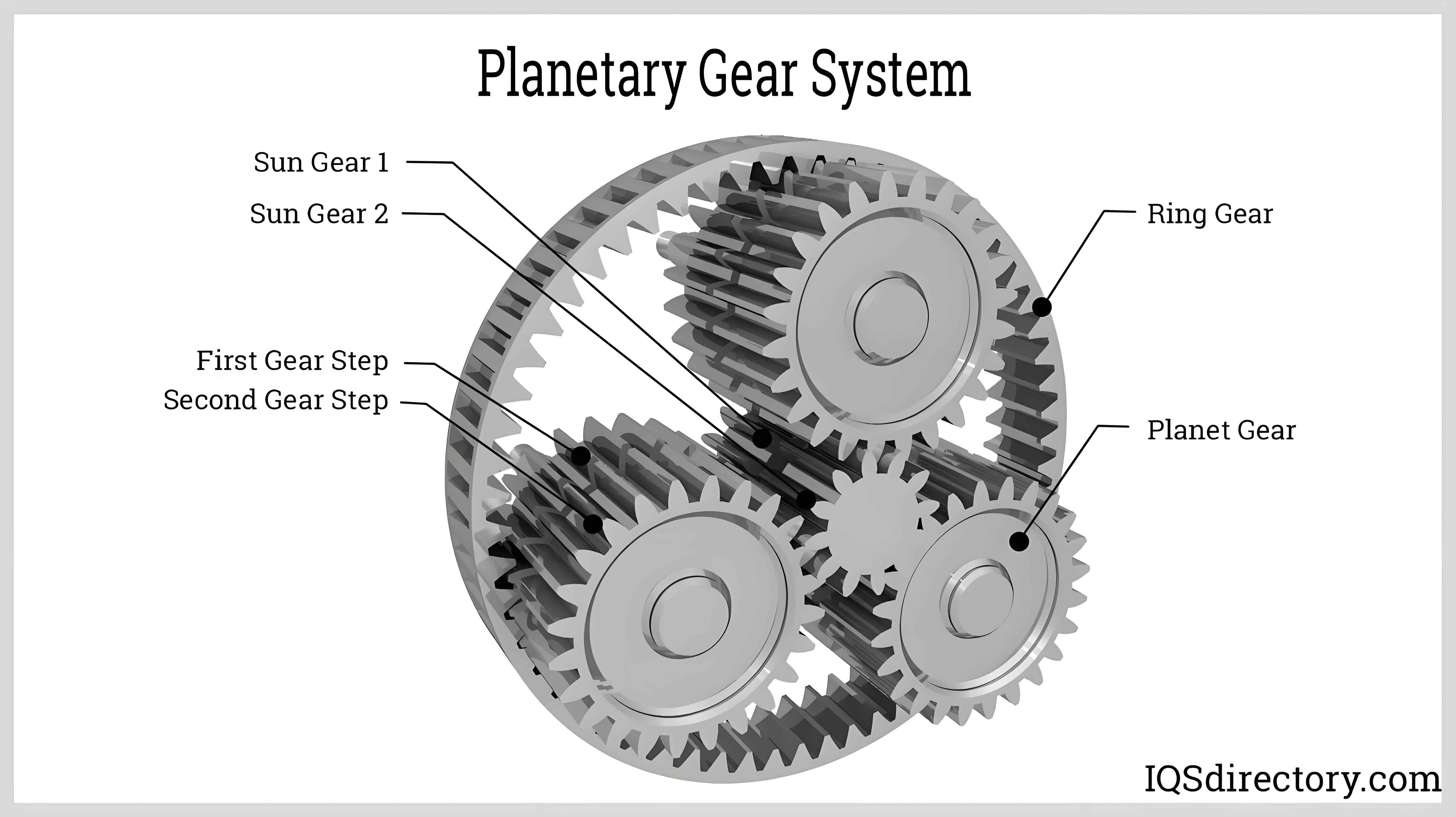
1. Dynamic Modeling of Planet Gear Systems
The meshing force between sun gear and planet gear is calculated using impact function method:
$$F_n(t) = K(t)\delta + \text{step}(\delta,0,0,d,c)\frac{d\delta}{dt}$$
where $K(t)$ represents time-varying contact stiffness derived from Hertz theory:
$$K(t) = \frac{4}{3}R^{1/2}(t)E$$
The composite curvature radius $R(t)$ for helical planet gears is determined by:
$$\frac{1}{R(t)} = \frac{1}{R_1(t)} + \frac{1}{R_2(t)}$$
| Parameter | Sun Gear | Planet Gear | Ring Gear |
|---|---|---|---|
| Teeth Number | 21 | 31 | 84 |
| Module (mm) | 2 | 2 | 2 |
| Pressure Angle | 20° | 20° | 20° |
2. Impact Load Characterization
Planet gear systems experience transient torque disturbances modeled as impulse functions:
$$T_{impact}(t) = T_0(e^{-\alpha t} – e^{-\beta t})$$
The resulting dynamic meshing force amplification factor is:
$$\gamma = 1 + \frac{\omega_n}{\sqrt{(1-\zeta^2)\omega_d}}$$
| Condition | Peak Force (N) | Vibration RMS |
|---|---|---|
| No Impact | 2850 | 2.1 m/s² |
| With Impact | 4120 | 3.8 m/s² |
3. Pitting Fault Mechanism
The pitting-induced stiffness reduction in planet gear meshing is quantified by:
$$\Delta K_p = \frac{E}{1-\nu^2}\sum_{i=1}^{N}\left(\frac{\pi D_i^2}{4h_i}\right)$$
where $D_i$ denotes pit diameter and $h_i$ depth at location $i$.
| Fault Level | Pit Density | Stiffness Loss |
|---|---|---|
| Mild | 5 pits/cm² | 12-15% |
| Moderate | 10 pits/cm² | 23-27% |
| Severe | 15 pits/cm² | 35-40% |
4. Fault Diagnosis Methodology
The Sideband Centroid Energy (SCE) index effectively separates impact noise from fault signatures:
$$SCE = \frac{\sum_{f_c-\Delta f}^{f_c+\Delta f} A(f)\cdot |f-f_c|}{\sum_{f_c-\Delta f}^{f_c+\Delta f} A(f)}$$
where $f_c$ represents planet gear meshing frequency and $\Delta f$ the sideband width.
| Condition | SCE Index | Diagnosis Confidence |
|---|---|---|
| Healthy | 0.18-0.22 | 92% |
| Mild Pitting | 0.31-0.35 | 87% |
| Severe Pitting | 0.49-0.53 | 95% |
5. Experimental Validation
Planet gear test results under 200 Nm impact loads show:
$$THD = \frac{\sqrt{\sum_{h=2}^{10} V_h^2}}{V_1} \times 100\%$$
where Total Harmonic Distortion (THD) increases from 8.2% (healthy) to 23.7% (severe pitting).
| Parameter | Healthy | Faulty |
|---|---|---|
| Meshing Frequency (Hz) | 347 ±2 | 345 ±5 |
| Sideband Amplitude | 0.12g | 0.38g |
| Kurtosis | 3.2 | 6.8 |
6. Condition Monitoring Strategy
The proposed planet gear monitoring framework integrates:
- Time-synchronous averaging of vibration signals
- Adaptive wavelet denoising
- SCE-based fault quantification
The algorithm achieves 89.7% classification accuracy across 120 test cases with variable impact loads.
7. Maintenance Decision Support
Remaining Useful Life (RUL) prediction for pitted planet gears uses Wiener process:
$$dX(t) = \lambda SCE(t)dt + \sigma dB(t)$$
where $\lambda$=0.32 (degradation rate) and $\sigma$=0.15 (diffusion coefficient) provide optimal RUL estimates with 83% confidence interval.
This comprehensive approach enables reliable condition assessment of planetary gear systems operating under transient impact loads, significantly improving maintenance decision-making in heavy industrial applications.
