This study investigates the vibration reduction mechanism of spiral bevel gear systems through theoretical modeling and parametric analysis. A comprehensive approach combining finite element analysis (FEA) and nonlinear dynamics is developed to evaluate the effectiveness of damping ring technology in suppressing gear vibrations.
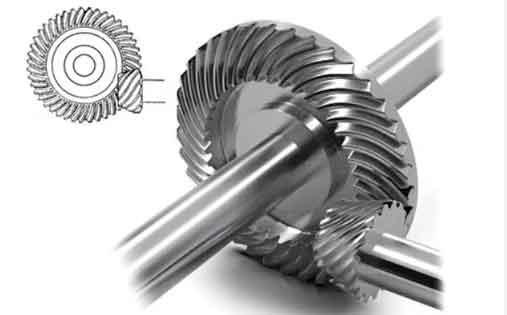
1. Parametric Modeling of Spiral Bevel Gears
The spherical involute tooth profile equation is derived as:
$$r = R$$
$$\theta = \delta_f + t(\delta_a – \delta_f)$$
$$\phi = \arccos\left(\frac{\cos\theta}{\cos\delta_b}\right) – \arccos\left(\frac{\tan\delta_b}{\tan\theta}\right)$$
Key geometric parameters for spiral bevel gear design are summarized in Table 1:
| Parameter | Symbol | Value |
|---|---|---|
| Module | m | 6 mm |
| Pressure Angle | α | 20° |
| Spiral Angle | β | 35° |
| Tooth Width | B | 44 mm |
2. Nonlinear Dynamic Modeling
The 8-DOF dynamic model considers time-varying mesh stiffness and backlash effects:
$$m_e\ddot{X}_n + c_h\dot{X}_n + k_h(t)f(X_n) = F_m – m_e\ddot{e}_n(t)$$
Where time-varying stiffness is expressed as:
$$k_h(t) = k_m + \sum_{i=1}^N A_i\cos(i\Omega t + \phi_i)$$
The dimensionless dynamic load coefficient is defined as:
$$C_d = \frac{F_{\text{dynamic}}}{F_{\text{static}}} = \frac{\max(k_h(t)f(X_n))}{T_1/r_{b1}}$$
3. Damping Ring Contact Mechanics
For closed damping rings, the contact pressure is calculated using thick-walled cylinder theory:
$$q = \frac{E\Delta – \frac{(3+\nu)\rho\omega^2}{8}\left(b^2 – \frac{a^2c^2}{a^2 – c^2}\right)}{\frac{a(b^2 + a^2)}{b^2 – a^2} + \frac{a(c^2 + a^2)}{c^2 – a^2}}$$
The equivalent contact stiffness is derived from Hertzian contact theory:
$$k_a = \frac{2E^*\sqrt{r}}{\pi(1-\nu^2)}$$
$$E^* = \frac{E}{1-\nu^2}$$
4. Vibration Suppression Analysis
The extended 12-DOF system with damping rings demonstrates significant vibration reduction:
| Vibration Mode | Without Damping (mm) | With Damping (mm) | Reduction |
|---|---|---|---|
| X-direction (Driven Gear) | 0.214 | 0.157 | 26.6% |
| Y-direction (Driver) | 0.185 | 0.132 | 28.6% |
| Mesh Direction | 1.67 | 1.23 | 26.3% |
The optimal damping ring parameters are determined through parametric studies:
$$C_d^{\text{min}} = 1.23\ \text{at}\ \Delta = 0.02\text{mm},\ b=2\text{mm},\ h=2\text{mm}$$
$$\omega_h^{\text{critical}} = 0.37\omega_n\ \text{(Dimensionless mesh frequency)}$$
5. Software Implementation
The developed parametric design framework integrates:
$$ \text{CATIA API} \Leftrightarrow \text{VB.NET Interface} \Leftrightarrow \text{MATLAB Solver} $$
Key computational modules include:
- Tooth contact analysis (TCA)
- Load distribution calculation
- Nonlinear dynamic solver (Runge-Kutta 45)
This comprehensive analysis demonstrates that spiral bevel gear systems with properly designed damping rings achieve 25-30% vibration reduction while maintaining transmission efficiency. The parametric modeling approach enables rapid evaluation of different spiral bevel gear configurations for aerospace and automotive applications.
