According to Newton’s second law, the dynamic equation of the system is established as follows
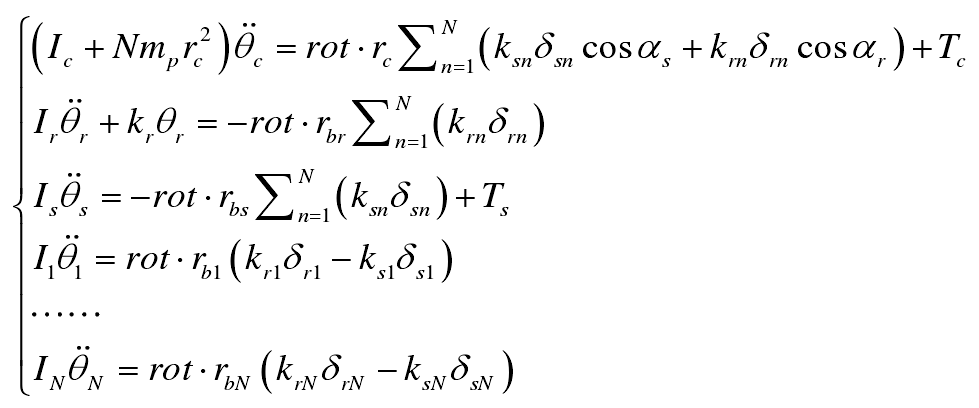
Where I (I = R, s, 1, 2,…) , n) is the moment of inertia of component I around its center of mass; MP is the mass of a single planetary gear, KSN is the time-varying meshing stiffness of the sun gear and the nth planetary gear; Krn is the time-varying meshing stiffness of the inner ring gear and the nth planetary gear; TC and TS are the external torques of the planet carrier and the sun gear respectively, and the positive and negative values are judged by the right hand rule.
The formula can be written in matrix form
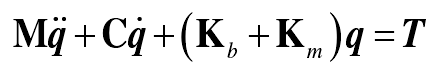
The matrix and vector in the formula are 3 + N dimensions, and the specific meaning of each symbol is as follows:
1) Q is the generalized coordinate vector of the system
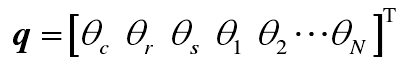
2) M is a mass matrix and a diagonal matrix
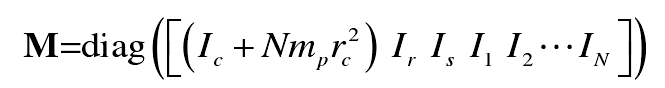
3) C is the damping matrix, using proportional damping
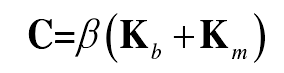
Where β is the proportional damping coefficient and is a constant.
4) KB is the support stiffness matrix and a diagonal matrix
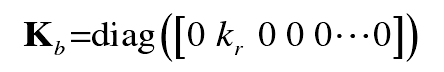
5) Km is the meshing stiffness matrix, in which the non-zero elements are
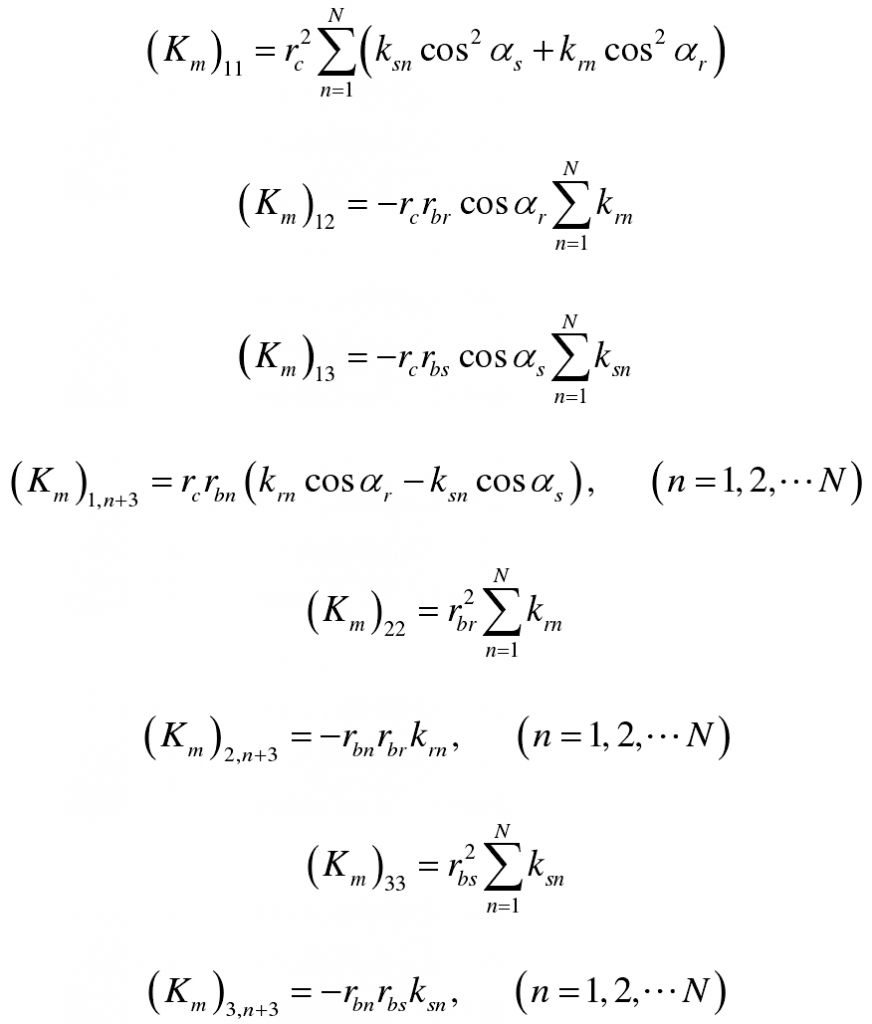
6) T is the external excitation torque vector
It should be noted that although the displacement projection of the sun gear and the inner gear ring relative to the nth planetary gear is related to the rotation direction of the sun gear (rot value), the meshing stiffness matrix of the planetary gear train does not change with the change of the rotation direction of the sun gear.


