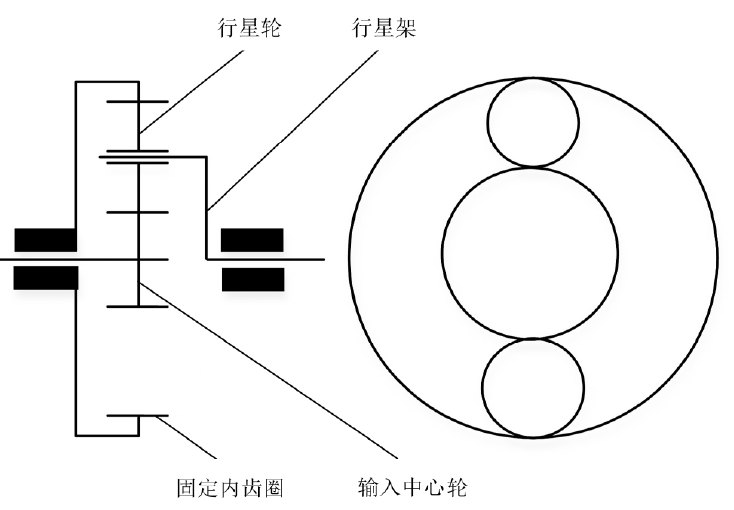
According to Lagrange equation, the dynamic differential equation of planetary transmission system can be deduced as follows
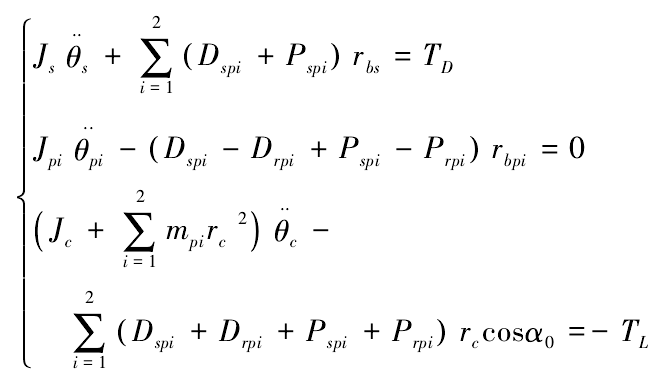
Among them, JS, JPI and JC are the moment of inertia of the center gear, the i-th planetary gear and the planet carrier respectively; RBS, rBPI and RC are the radius of the indexing circle of the center gear, the planet gear and the planet carrier respectively; P and D are the elastic meshing force and viscous meshing force of the gear pair respectively, and their mathematical expressions are as follows
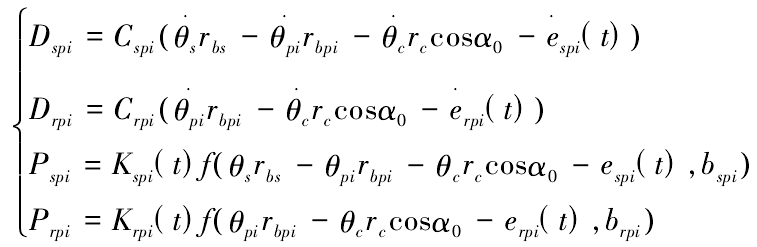
ESPI (T) and Erpi (T) are the comprehensive meshing errors of each gear pair, which can be expressed by the first harmonic of meshing function.
The relative displacement coordinate is introduced into the dynamic differential equations of planetary transmission system to eliminate the coupling term in the equations
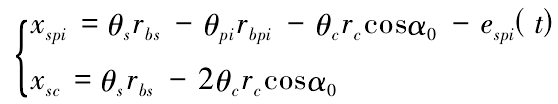
The dynamic differential equations of the transmission system are normalized, and the dimensionless differential motion equations of the planetary transmission system are obtained.