For gear transmission system dynamics by physical model to the transformation of the mathematical model, and to establish the mathematical model of numerical solution method, scholars have launched research both at home and abroad, and according to the different response characteristics and different degrees of freedom, the establishment of an independent correlation analysis model, such as the type torsional vibration model of three degrees of freedom (FIG. (a)), not considering the gear pair meshing of friction type coupling vibration model (FIG. (b)), taking into account the friction gear pair meshing type coupling vibration model (FIG. (c)) and elastic coupling system vibration model of bearing housing and rotor (FIG. (d) and (e)).
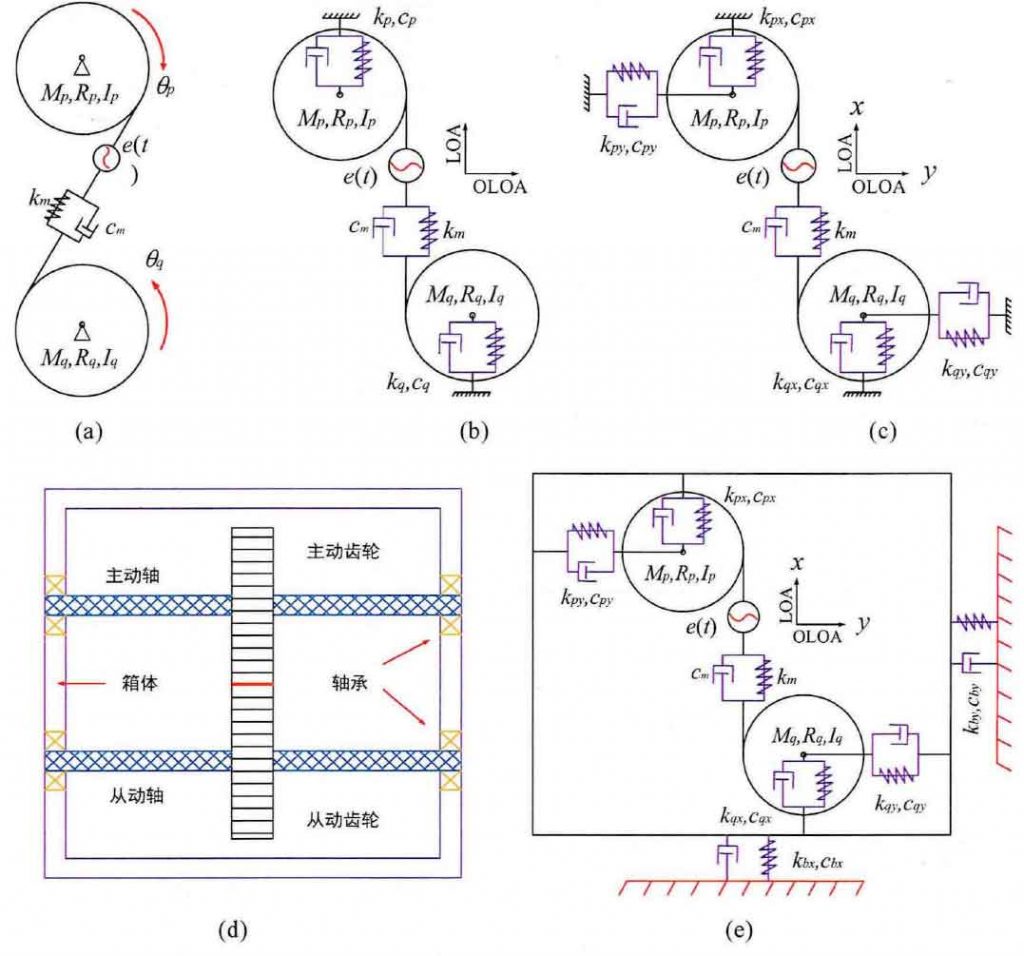
If the drive shaft, supporting bearing and box in the gear system are compact and have large relative stiffness, and the elastic deformation is negligible, the mathematical model of pure torsional vibration as shown in Fig. (a) can be adopted. The simplified mathematical model of pure torsion can actually study the influence of single factors (such as friction coefficient, clearance, modification, etc.) on the dynamic response characteristics of the system, and at the same time can visually display the side band modulation and generation mechanism of vibration response signals. Li Yongzhuo et al. established a fixed-axis torsional vibration analysis model, considered linear and nonlinear excitation factors respectively, and studied the frequency response characteristics of the system under normal state and fault, as well as the generation and modulation mechanism of vibration response signal side frequency band. The results show that the nonlinear excitation factors can form higher order meshing frequency components than the linear excitation factors. The rotation frequency of the fault gear is obvious on both sides of the meshing frequency and has the modulation side frequency band effect. Wang Sanmin et al. used torsional vibration model to study the chaotic and bifurcation response of spur gear pair system considering tooth surface friction and tooth side clearance, and adopted the 5-6 order Runge-Kutta variable step method to solve and calculate the system.
The results show that the existence of the friction coefficient makes the response of the dynamic system produce the mixed purity phenomenon in advance, accompanied by a strong superharmonic and subharmonic component, and has little effect on the maximum Lyapunov exponent, showing a slight decrease trend, that is, the degree of chaos is slightly reduced. Chen Siyu et al. adopted this simplified model to establish three different clearance excitation modes (constant clearance, time-varying clearance and random clearance) to study the influence of toothed clearance on the response of the system. The results show that at low speed, each index of the system response increases with the increase of friction coefficient. The increase of time-varying clearance and random clearance will lead to chaos phenomenon in the early stage of the system, and the system response is dominated by high frequency components. At the same time, it also studies the influence of tooth profile modification, the dynamic properties of gear modification quantity and modification length, which can accurately grasp the actual operation performance of gear, and it is of great significance to select the optimal modification size in the later stage. Tang He et al. discussed in detail the vibration and noise spectrum characteristics of the basic gear geometrical parameters (module, tooth number, tooth width, etc.), as well as the influence of parts processing errors and assembly state errors on the system vibration. Zhang Linlin et al. studied the effect of internal excitation (stiffness and error), and analyzed the noise influence of internal excitation on system vibration by using the calculation formula of Kato correction of noise intensity.
