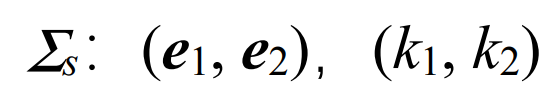Spiral bevel gear pair conjugate pinion tooth surface Σ 1 modification, in the field of calculation point m, it is bound to be able to construct a modified tooth surface of spiral bevel gear pinion that is out of tangent in the other neighborhood tangent to point m, which is called contact tooth surface Σ s. The corresponding principal direction and principal curvature are recorded as:
1. Topology of tooth surface contact area of spiral bevel gear
stay Σ s、 Σ The difference surface constructed along the normal direction between 1 is called ease off surface Σ d. It reflects the loss of tangent of conjugate tooth surface of spiral bevel gear. In the field of point m, this surface can be replaced by a close surface with the shape of formula (5):
Where, ZD direction is the same as the normal direction of point m, (XD, YD), (KA, KB) are differential tooth surfaces respectively Σ Principal direction and principal curvature of D. They determine the size, shape and direction of the contact area.
According to the theorem, the close surface represented by the formula can replace the ease off difference tooth surface for surface analysis. The contour of the formula is an elliptic curve, ZD = 0.006, and the contour of 35mm represents the tooth surface contact area of spiral bevel gear (Fig.). Assuming that the lengths of the major and minor axes of the contact area ellipse are a and B respectively, the following formula can be obtained:
The asymptotic direction in the meshing movement of the two tooth surfaces of spiral bevel gear, that is, the tangent direction of the contact path of the spiral bevel gear tooth surface, and the included angle Q with the first principal direction XD of the ease off surface is:
The normal curvature KS in this direction reflects the loss of tangent of the tooth surface along the contact path, and its normal section is a parabola, that is:
The formula represents the first derivative value M12 ‘of the instantaneous transmission ratio function of large and small wheels respectively( φ 1) Transmission error curve, but the formula uses length unit instead of angle unit.
Inclination of a given contact ellipse λ (XD the included angle in the direction of ex, which reflects the inner diagonal degree of the contact mark), find the ease off surface Σ d: Curvature and torsion in X, Y direction (ax, ay, CX):
For spiral bevel gear, the pinion touches the tooth surface Σ s: Curvature and torsion in (ex, ey) direction (Ki, kJ, τ x) For:
Principal direction principal curvature Σ s: (E1, E2), (K1, K2) are:
2. Preset contact parameters
When the contact parameters (a, b) are given, λ) After that, the tooth surface of the small wheel can be calculated by the formula Σ S calculation point m: (E1, E2), (K1, K2). And the calculation point m: R1 (U0, θ 0) 、n1 ( θ 0) known. Uniformly record the contact parameters of calculation point m as: