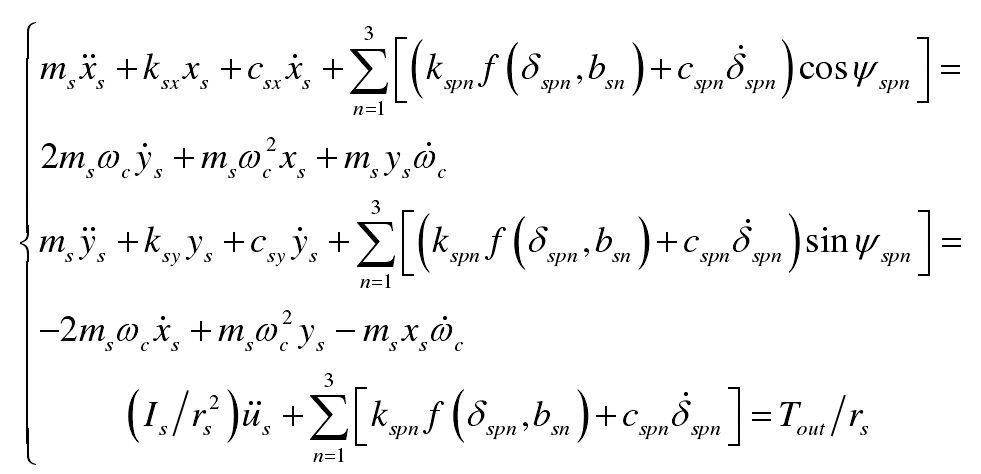The planetary gear transmission system studied in this paper has fixed inner gear ring, planetary carrier and sun gear as input and output components of power and motion respectively. It is assumed that the mass of planetary carrier, inner ring gear, planetary gear and sun gear are MC, Mr, Mn and MS respectively, and the moment of inertia is IC, IR, in and is respectively.
1、 According to the analysis of the relative motion relationship of each component in the previous section and Lagrange equation, the linear differential equation of translational torsional dynamics of planetary gear transmission system can be listed
(1) Planet carrier:
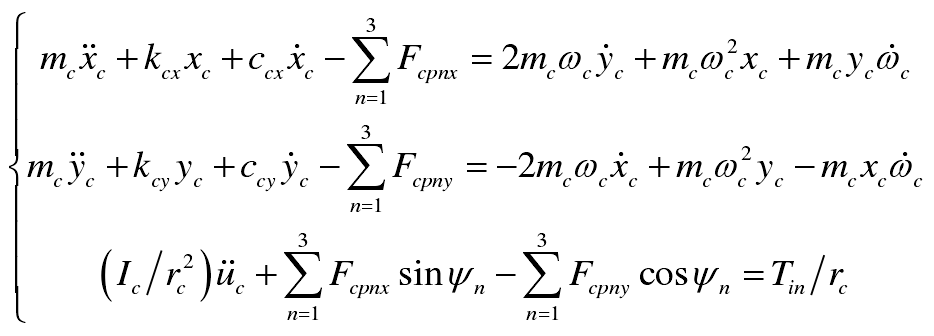
(2) Inner ring gear:
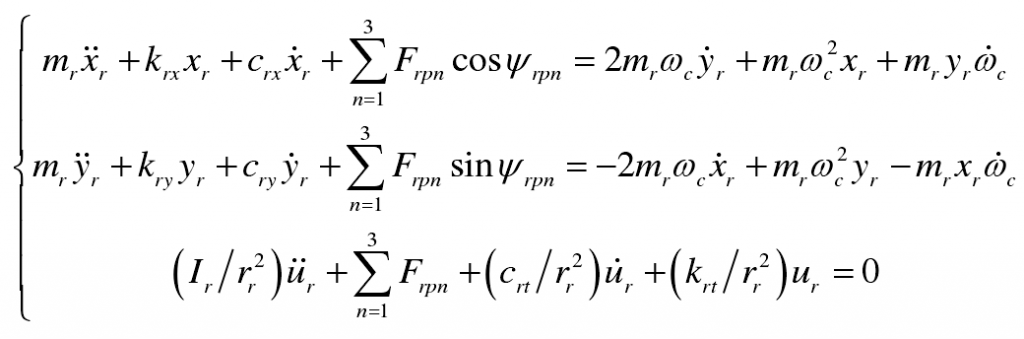
(3) Planetary gear:
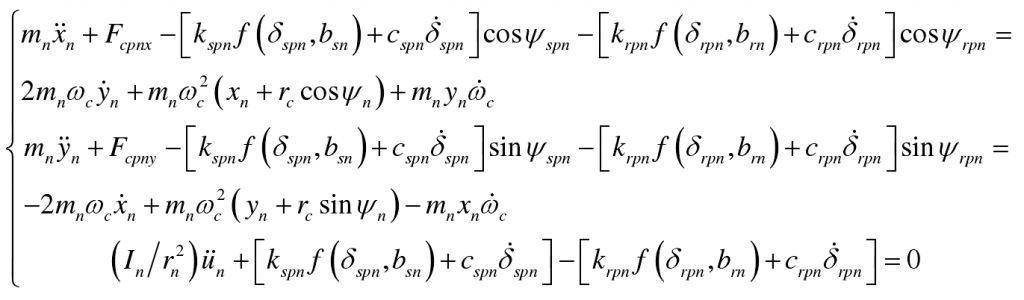
(4) Sun wheel:
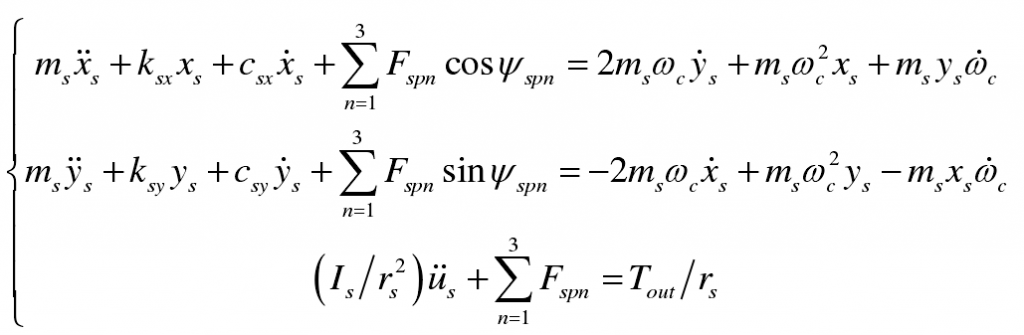
2、 Taking into account the backlash, transmission error and time-varying meshing stiffness, the nonlinear dynamic differential equation of the system can be deduced as follows:
(1) Planet carrier:
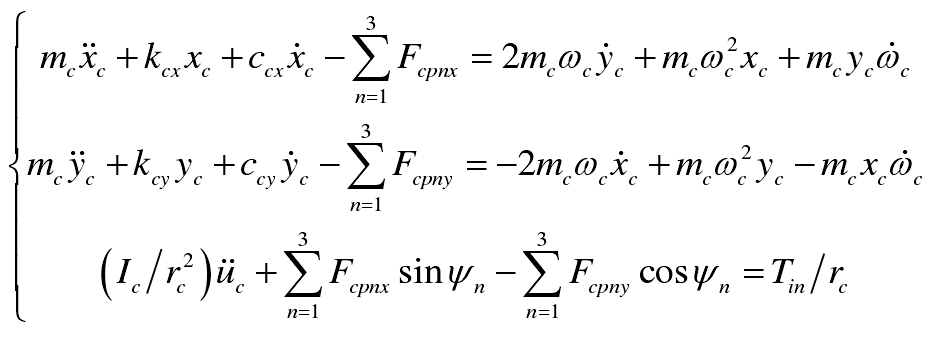
(2) Inner ring gear:
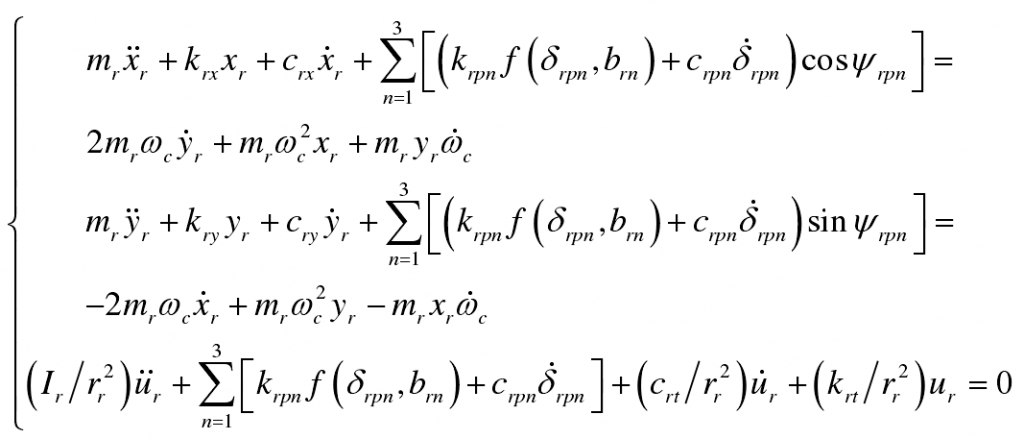
(3) Planetary gear:
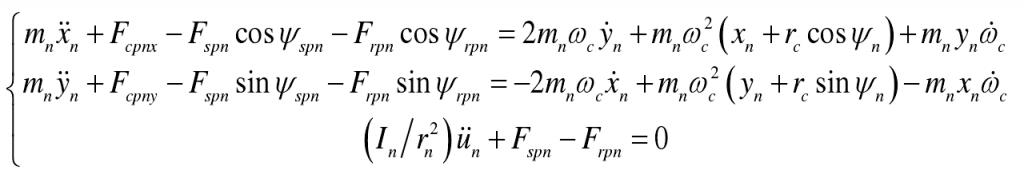
(4) Sun wheel: