As shown in the figure, it is known that the input power P1 of the high-speed stage of the two-stage helical cylindrical gear reducer is 6.2kw, the speed n1 is 1450r / min, the total transmission ratio I is 31.5, the gear width coefficient is ψ d = 0.5, and the load coefficient K is 1.3. The gear material and heat treatment are as follows: big gear 45 steel, normalizing treatment, small gear 45 steel, quenching and tempering treatment. The surface hardening temperature is 45hrc. It is required to determine the gear transmission scheme according to the minimum total center distance.
Solution: according to the gear material and heat treatment specification, the calculation results show that σ H = 518.75mpa, [σ F] 1.3 = 153.5mpa and [σ F] 2.4 = 141.6mpa. The relevant data are substituted into the strength calculation formula
High speed shaft torque T1 = 41690;
Intermediate shaft torque T2 = 40440;
High speed shaft gear load factor K1 = 1.225;
Low speed shaft gear load factor K1 = 1.204.
1.Establish the mathematical model of optimal design
Selected variables: take the parameters related to the evaluation result of total center distance α Σ as the calculation variables
2 objective function
The objective function of minimizing the total center distance of gear transmission is as follows
3 constraints
① According to the formula, the constraint equation of tooth surface fatigue strength is obtained
② According to the formula, the constraint equation of fatigue strength of tooth root can be obtained
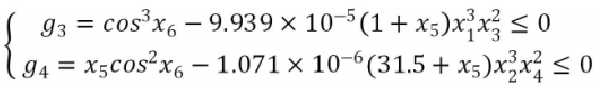
③ According to the formula, the constraint equation of two-stage (high-speed and low-speed) big gear without interference can be obtained
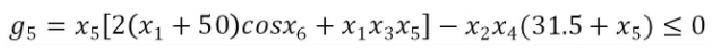
④ Other constraints (listed part): according to the power size, speed, modulus value and other factors of reducer gear, reasonable consideration should be given to the number of gear teeth, diameter of dividing circle, axial force, transmission ratio range and other conditions.
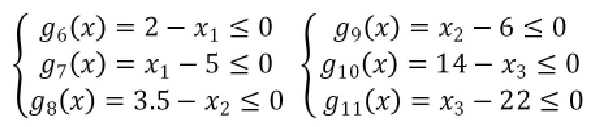
4.The realization process of MATLAB
① The center distance expression and constraint conditions of the above reducer are solved by using fimicon in MATLAB
xi=2.0 3.5 18.4 16.0 6.3 8.0
② Analysis of optimization results.
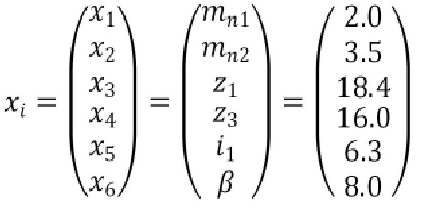
1) The results show that Mn1 = 2mm and Mn2 = 4mm.
2) The results show that Z1 = 18.
3) From the transmission ratio of high-speed stage I1 = 6.3119, the tooth number of high-speed stage big gear Z2 = i1z1 = 6.3119 × 18 = 113.6142 is obtained, taking Z2 = 114.
4) If I2 = I / I1 = 31.5/6.3119 = 4.9906, then the number of teeth of low-speed stage gear is Z4 = i2z3 = 4.9906 × 16 = 79.8492, taking Z4 = 80.
5) The total center distance is α Σ.
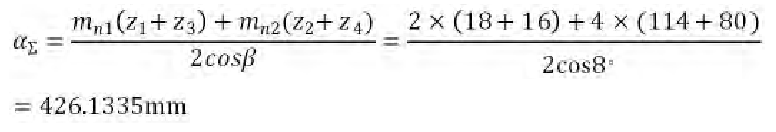
After rounding, the total center distance of cylindrical reducer is αΣ = 425mm.

