The tooth surface of the helical involute cylindrical gear with the number of teeth of Ng is taken as the theoretical tooth surface, and the tooth surface of the helical tooth surface gear of the straight tooth turning cutter with the number of teeth of Ns is taken as the turning tooth surface. The normal distance difference between the turning tooth surface and the theoretical tooth surface is defined as the discrete point error of the tooth surface. In this paper, the tooth surface of helical gear is divided into rectangular meshes along the direction of tooth width and tooth height. The same mesh points correspond to the normal distance of tooth surface points δ It is expressed as the dot product of the difference between the two vector diameters and the internal normal vector, namely:
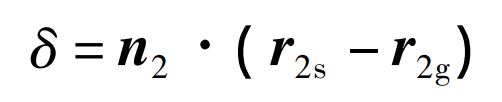
Where, n2s is the internal normal vector of any point on the theoretical tooth surface of helical gear; R2s and r2g are the radial vectors of the turning tooth surface and the theoretical tooth surface at the same mesh point.
| Object | Parameters | Example 1 | Example 2 |
| Tooth turning tool | Number of teeth Ns | 27 | 32 |
| Tooth turning tool | Modulus m (mm) | 3.25 | 3.25 |
| Tooth turning tool | Pressure angle α ( °) | 20 | 20 |
| Hypothetical shape-producing wheel | Number of teeth Ng | 24 | 24 |
| Hypothetical shape-producing wheel | Normal modulus mn (mm) | 3.25 | 3.25 |
| Hypothetical shape-producing wheel | Normal pressure angle α n ( °) | 20 | 20 |
| Hypothetical shape-producing wheel | Helix angle β ( °) | 15 | 25 |
| Hypothetical shape-producing wheel | Rotation direction | Dextral rotation | Dextral rotation |
| Helical gear | Number of teeth N2 | 72 | 72 |
| Helical gear | Minimum internal radius R1 (mm) | 117 | 125 |
| Helical gear | Maximum outer radius R2 (mm) | 137 | 147 |
| Helical gear | Tooth width L (mm) | 20 | 22 |
| Helical gear | Rotation direction | Dextro rotation | Dextro rotation |
| Axial intersection angle | Size (°) | 15 | 25 |
| Axial intersection angle | Deviation | Left | Left |
Take the axis O2 z2 of the helical gear as the axis and L1 as the radius to make a cylindrical surface, respectively intercept the two tooth profiles of the turning tooth surface and the theoretical tooth surface, and project them to the plane x2O2 y2, plane x2O2 z2 and plane y2O2z2 for tooth profile error analysis.
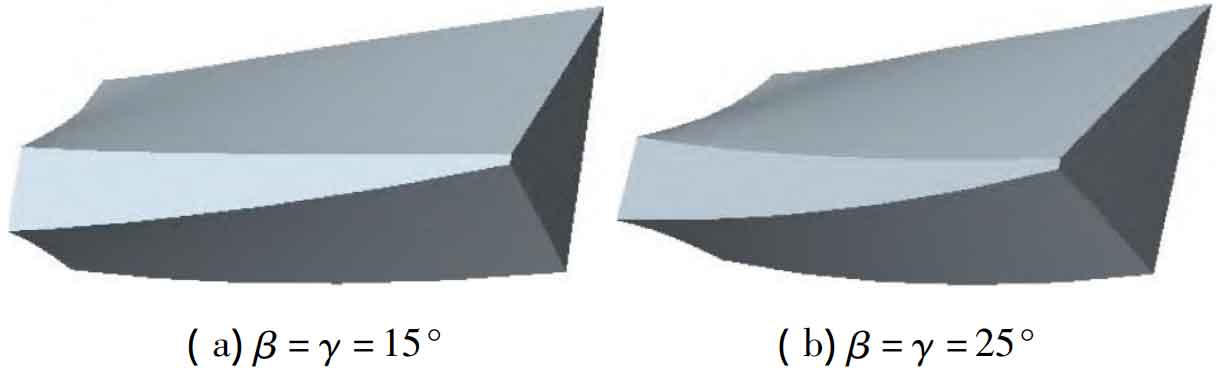
When the imaginary spiral angle of the generating wheel β And the intersection angle between the tooth turning tool and the imaginary shape-producing wheel shaft γ When equal, the tooth width of the turning tooth surface of the helical tooth surface gear is equal to the theoretical tooth surface. The parameters of the turning tool, the imaginary generating wheel and the helical tooth surface gear in Example 1 and Example 2 are shown in the table. The teeth of the helical tooth surface gear machined by the turning tool and the imaginary generating wheel with different shaft intersection angles are shown in the figure.
