The sampled signals are analyzed and processed in DH5922 dynamic signal test and analysis system software of Donghua Test. Figure 1 shows the time domain response test results of reducer vibration acceleration under the above typical working conditions. When the load torque is 80 N · m, the input speed is 600 r/min, 1400 r/min, 2200 r/min respectively, and the corresponding RMS values of vibration acceleration are 0.269 m/s2, 0.818 m/s2, 1.537 m/s2. The vibration acceleration value increases, and the vibration intensity of the reducer increases; When the input speed is 1400 r/min, the load torque is 40 N · m, 80 N · m, and 120 N · m respectively, and the corresponding RMS values of vibration acceleration are 0.701 m/s2, 0.818 m/s2, and 0.929 m/s2. The vibration acceleration values increase slightly.
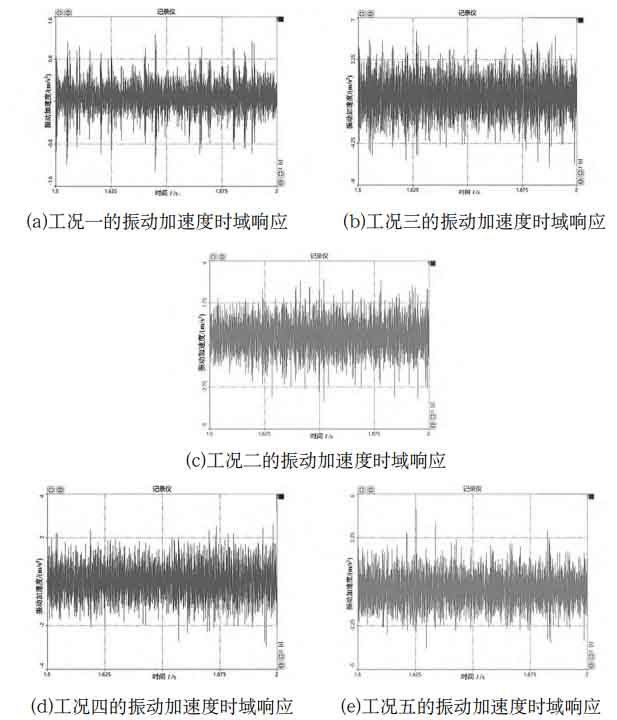
Table shows the root mean square value of the vibration acceleration simulation value and the experimental value of the linear conjugate planetary gear reducer with small tooth difference. The RMS error of the above typical working conditions is within 10%. It can be concluded that the vibration acceleration test results are in good agreement with the simulation results, and the experimental results verify the reliability of the vibration characteristics simulation of the planetary gear reducer.
| Working condition | 600 r/min,80 N·m | 1,400 r/min,80 N·m | 2,200 r/min,80 N·m | 1,400 r/min,40 N·m | 1,400 r/min,120 N·m |
| Simulated RMS value/(m/s2) | 0.296 | 0.879 | 1.693 | 0.742 | 0.977 |
| Experimental RMS value/(m/s2) | 0.269 | 0.818 | 1.537 | 0.701 | 0.929 |
| Relative error/% | 9.12 | 6.94 | 9.21 | 5.53 | 6.96 |
The time domain signal can directly show the trend of vibration acceleration changing with time and the intensity under different working conditions, but the vibration signal has distortion and modulation in the actual test. Therefore, in order to more effectively study the vibration characteristics of the reducer, it is necessary to carry out the frequency domain analysis of the signal. Fast Fourier transform is applied to the time-domain signal of vibration acceleration to obtain a spectrum function with the independent variable being frequency and the dependent variable being frequency amplitude, representing the linear distribution of the amplitude of each harmonic component in the time-domain signal with frequency.
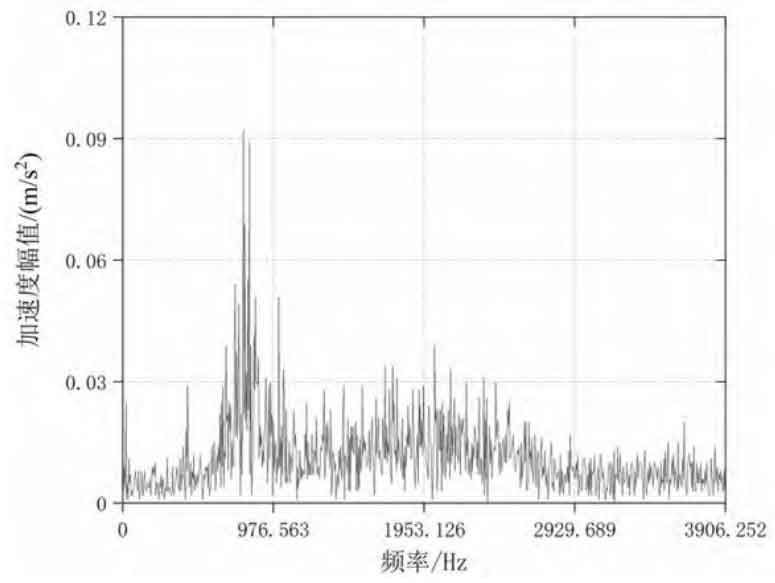
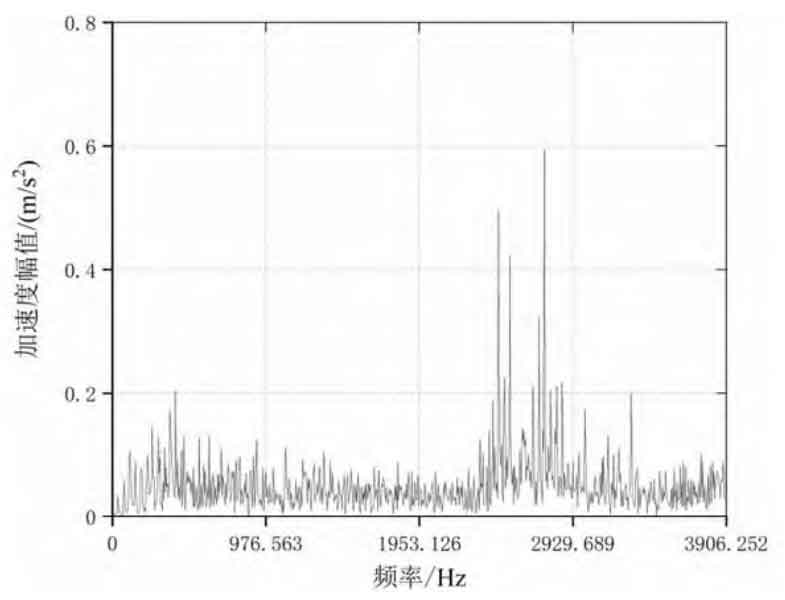
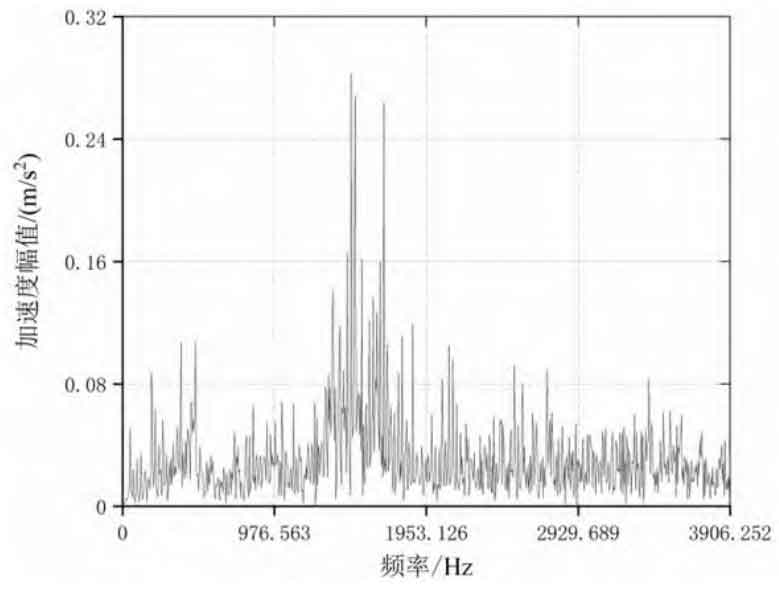
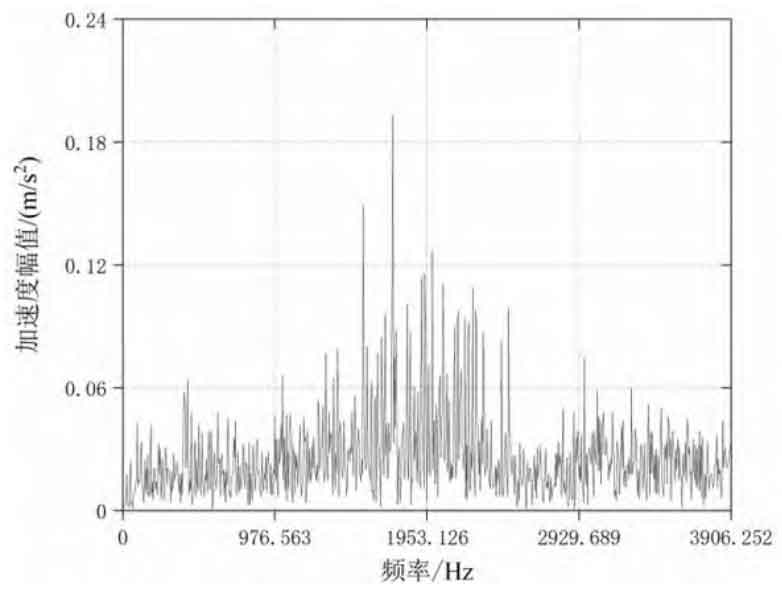
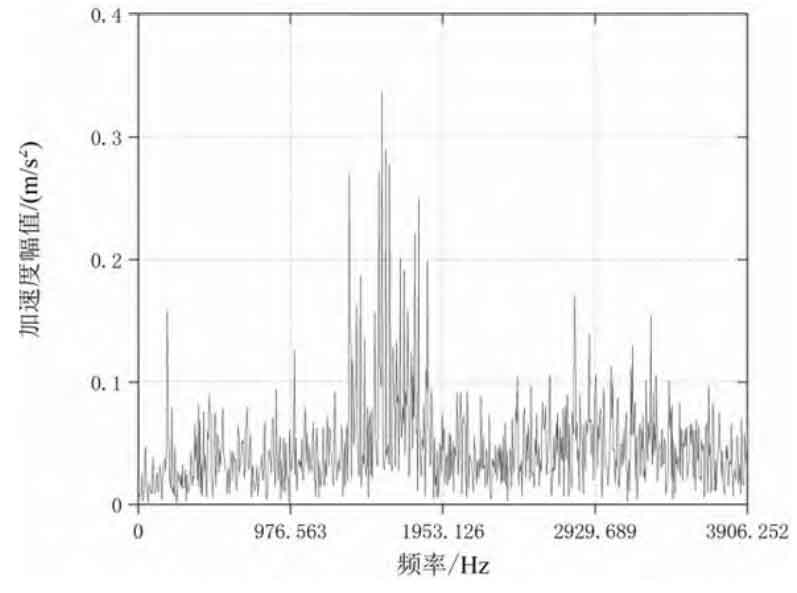
Figure 2 shows the frequency domain analysis results of reducer vibration acceleration under typical working conditions. The main frequency components in the spectrum are: input shaft rotation frequency, gear pair meshing frequency and its higher harmonic frequency, vibration frequency caused by installation coaxiality error, various distortion and modulation frequencies. The large amplitude response of vibration acceleration in the spectrum is due to the impact of eccentric inertial motion caused by eccentric structure of input shaft on bearing ball and meshing impact of gear pair. As shown in Figure 2 (a), when the input speed is 600 r/min, the peak frequency in the spectrum is 765.25 Hz, and there are small peaks at 60 Hz on the left and right sides of the peak point; As shown in Figure 2 (c), Figure 2 (d) and Figure 2 (e), when the input speed is 1400 r/min, the peak frequency is similar, the average value is 1718.63 Hz, and there are small peaks at 80 Hz on the left and right sides of the peak point; As shown in Figure 2 (b), when the input speed is 2200 r/min, the peak frequency in the spectrum is 2698.63 Hz, and there are also small peaks at 80 Hz on the left and right sides of the peak point. In conclusion, the frequency distribution of vibration acceleration signal is positively correlated with the input speed. With the increase of operating speed, the theoretical meshing frequencies are 720 Hz, 1680 Hz and 2640 Hz respectively, and the errors between the theoretical and experimental meshing frequencies are 6.28%, 2.26% and 2.19% respectively. Within a reasonable range, the theoretical meshing frequency value is relatively consistent with the experimental value, and there is no overlap with the natural frequencies of each order in the modal analysis, No resonance occurs.