Firstly, the finite element model of rocker box is established in ABAQUS, and its mass matrix and stiffness matrix are extracted, which are called original matrix. In order to facilitate the mesh generation, the local details (such as chamfer and threaded hole) of the 3D box model are simplified. The element type is tetrahedral solid element, and the element generation method is free mesh generation. After the grid independence test, the final grid size is 65 mm, the total number of cells is 67890, and the total number of nodes is 17501. The nodes of the rocker box are divided into interface nodes and internal nodes: the interface node is the coupling interface between the rocker box and other parts of the system, which plays the role of transferring displacement and load; the internal node is the node except the interface node, which is only affected by internal force and inertial force. In ABAQUS, the nodes on the inner surface of the shaft / bearing hole on the rocker box are connected to the center of the bearing hole through rigid units, and 17 interface nodes are obtained, each node has 6 degrees of freedom; there are 17484 internal nodes, each node has only 3 translational degrees of freedom, and the rocker box has a total of 52554 degrees of freedom, as shown in Figure 2.4. InP file is a text file generated by ABAQUS, which contains a complete description of the whole finite element model and is a bridge between the preprocessor and the solver to transfer data. By using the keywords matrix general and matrix output to edit the InP file, the mass matrix and stiffness matrix of the rocker box can be extracted.

Then, the fixed interface mode synthesis method (Craig Bampton method) is used to condense the original matrix extracted in the previous step, and the result is called condensing matrix. The mathematical essence of mode condensation is linear space basis transformation, that is to transform the displacement of the object in the physical coordinate system into the modal coefficients in the modal coordinate system. If the number of independent modes selected by the basis transformation is equal to the number of degrees of freedom of the system, the accurate transformation result can be obtained, which is called complete transformation, but the complete transformation does not achieve the purpose of reducing the degrees of freedom. According to the vibration theory, when the external excitation frequency is close to a certain natural frequency, the contribution of this mode to the vibration response is larger; when the external excitation frequency is far away from a certain natural frequency, the contribution of this mode to the vibration response is smaller. Experience shows that the high frequency component of excitation is less in practical engineering problems, and the accurate results can be obtained by omitting the influence of high-order modes. Therefore, the Craig Bampton transformation is carried out to retain the first k-order principal modes. After the transformation, the internal node displacement of the finite element model is expressed as the superposition of the k-order modes, and the interface nodes are still physical coordinates

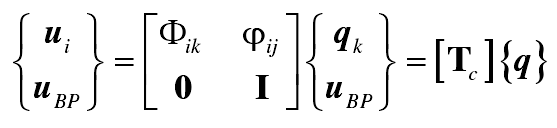
In the formula, UI is the degree of freedom of internal nodes; Ubp is the degree of freedom of interface nodes; Φ IK is the retained first-k order principal mode, which indicates the relative application of internal nodes to interface nodes; ψ ij is the constraint mode, which indicates the implicated motion of internal nodes caused by the unit displacement of interface nodes in a specific degree of freedom while the displacement of other degrees of freedom is zero; I is the unit matrix; QK is the constraint mode Is the modal coordinate; TC is the Craig Bampton transformation matrix.

To sum up, the reduction operation of the original matrix of the rocker box structure is as follows:

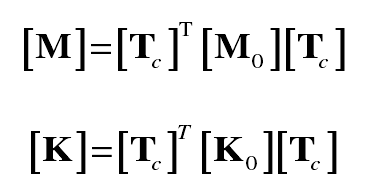
Where, M0 and K0 are the original mass matrix and original stiffness matrix extracted from ABAQUS, which are square matrices of order 52554; m and K are condensed mass matrix and condensed stiffness matrix. In this paper, there are 17 interface nodes with 102 (17 × 6) interface degrees of freedom, and the first 60 order principal modes are selected. Therefore, the reduced matrix is a square matrix of 162 order, and its order is greatly reduced compared with the original matrix.