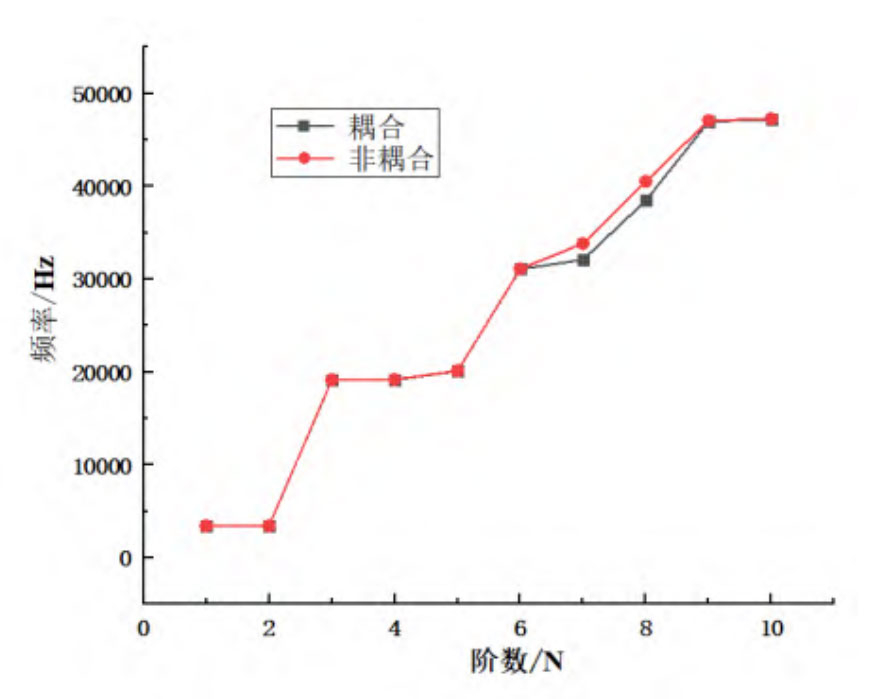
Establish data transmission for the distributed load pressure on the rotating pair obtained from Fluent analysis, and import it into Workbench Structural for pressure loading. The pressure distribution is shown in Figure 1.
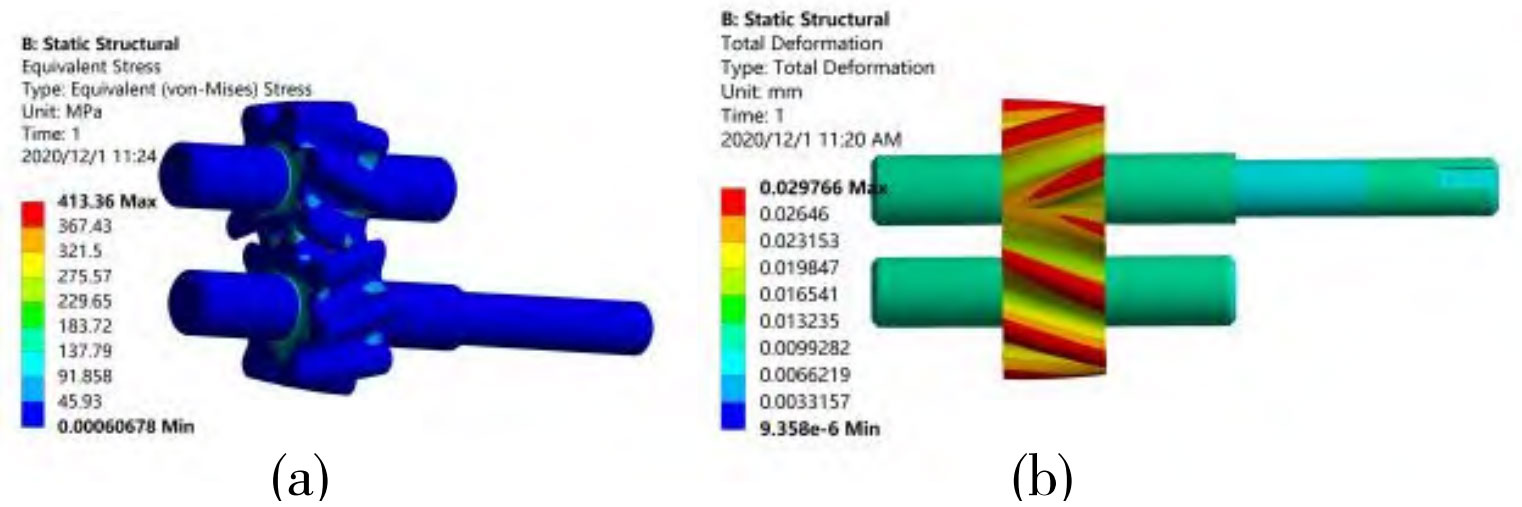
From the analysis, it can be seen that the equivalent stress and maximum deformation distribution areas of the rotor are basically the same in both coupled and uncoupled cases. From Figure 2, it can be seen that the maximum deformation of the rotor of the double arc helical gear pump is about 0.029242mm, and the maximum deformation occurs near the wheel edge of the rotor. The small deformation at the hub of the double arc helical gear pump rotor causes an amplification of the deformation at the rotor flange, which is the main factor causing the large deformation of the rotor flange of the double arc helical gear pump. From Figure a, it can also be seen that the maximum equivalent stress occurs near the meshing of the rotor, with a maximum equivalent stress of approximately 405.87MPa. After cyclic stress cycling, the rotor is prone to fatigue damage at the cross-sectional position. At this point, the safety factor is:
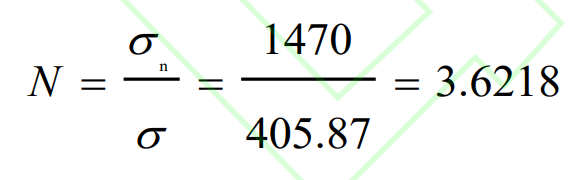
In the equation: σ N is the allowable stress.
The safety factor at the maximum contact stress is greater than the minimum safety factor of 2.5, so the strength and stiffness meet the requirements.
(b) Displacement and deformation distribution of rotating pair
At the outer edge of the rotor, the tensile deformation caused by centrifugal force is very small, while the deformation caused by flow field pressure and rotor torque is relatively large. This indicates that the centrifugal force of the double arc helical gear pump rotor has a small impact on it, but the influence caused by fluid force and torque is relatively large. Meanwhile, due to the maximum pressure occurring at the engagement position of the oil outlet rotor and the minimum negative pressure occurring near the engagement position of the oil inlet rotor, when it vibrates, it is easy to cause stress concentration in the rotor at the hub, becoming the maximum equivalent stress distribution area of the rotor.

As shown in Figure 3, in order to investigate the influence of load before and after fluid structure coupling on the maximum deformation and maximum stress of the rotating pair, an experimental testing device was built to test the double arc helical gear pump, in order to verify the reliability of the simulation results. When the load pressure (oil outlet pressure) is 15MPa, 20MPa, 25MPa, and 30MPa respectively, and the rotor speed is 10000r/min, analyze the variation curve of the rotating pair of the double arc helical gear pump.
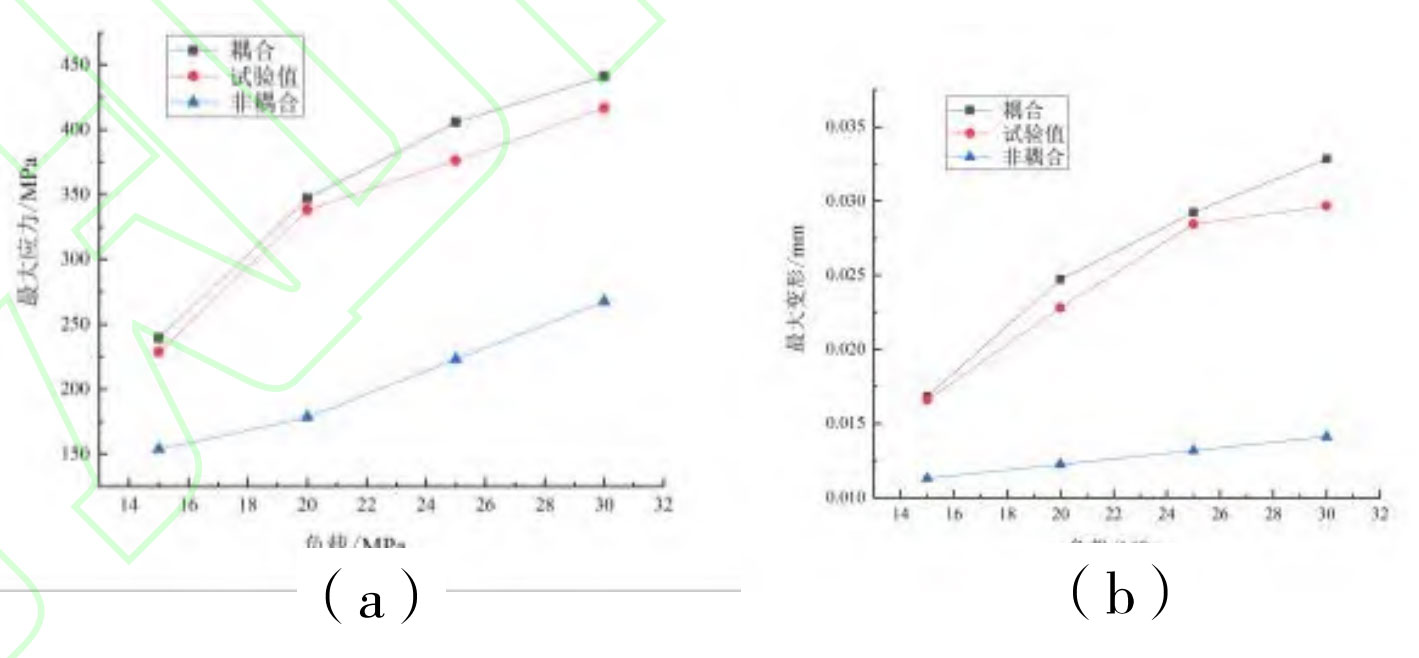
(b) Curve of maximum deformation change of rotating pair
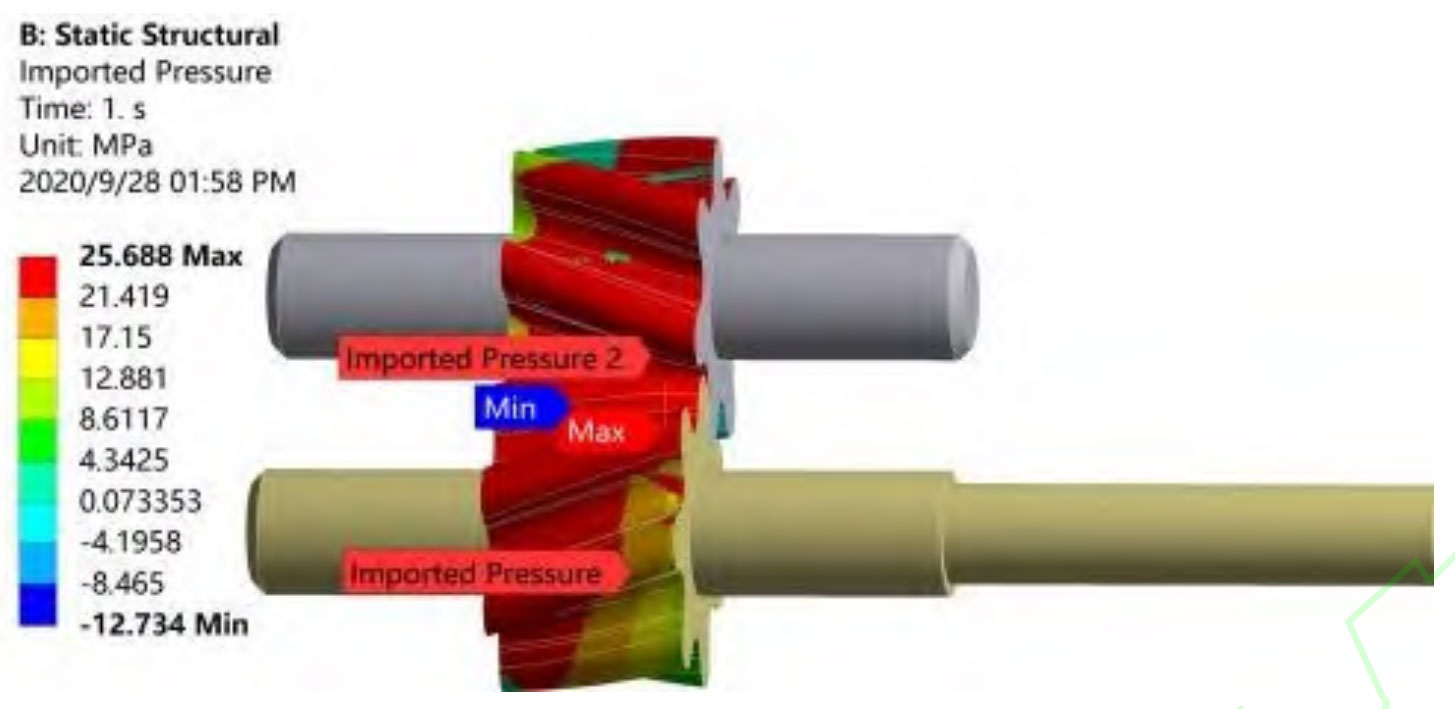
From Figure 4, it can be seen that the coupling and non coupling results are compared under different loads. The load has a significant impact on the maximum deformation and stress of the rotor under coupling conditions, but the maximum equivalent stress still meets the requirements of material fatigue limit and yield strength. At the same time, there is a significant difference between the maximum deformation and stress values before and after coupling, with a maximum deformation difference of 0.016063mm and a maximum equivalent stress difference of 187.72MPa. However, the maximum deformation position and stress concentration position are basically the same. Due to the changes in the fluid domain structure caused by the internal flow of fluid during the coupled calculation process, which have an impact on the rotor motion, the actual mechanical characteristics of the double arc helical gear pump rotor can be better reflected than the non coupled results. Figure 5 shows the comparison of the first 10 modal frequency distributions of the rotor of a double arc helical gear pump under coupled and uncoupled conditions. From the comparison results, it can be seen that there is a certain difference in natural frequencies between the two situations, but the difference is small.