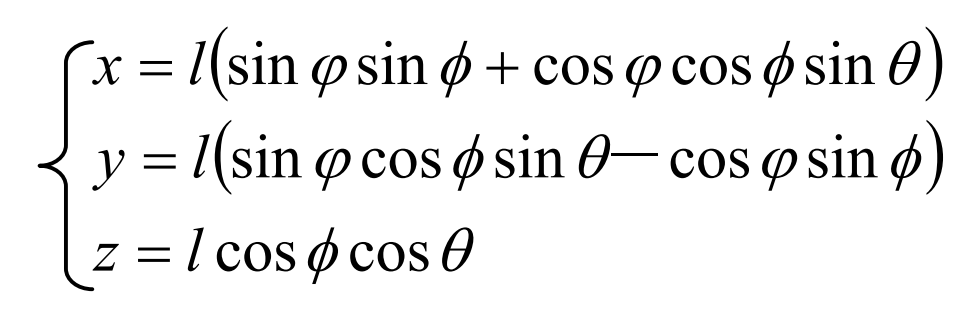The establishment of three-dimensional model of spur bevel gear is the basis of dynamic simulation analysis. The accuracy of solid model will affect the following dynamic analysis results. The tooth profile of bevel gear is a spatial spherical involute with complex topological structure, so the general three-dimensional modeling software can not directly complete the accurate modeling of spur bevel gear. Some scholars use tracing point fitting method or plane involute to realize the modeling of spur bevel gear. The models built by these methods are not accurate enough, so they can not get accurate simulation and analysis results.
Different from other gear transmission, the relative meshing motion of spur bevel gear is spherical motion, and the shape of tooth profile is spherical involute. Therefore, it is necessary to understand how the spherical involute is formed and the meaning of various parameters in the spherical involute equation, so as to solve the spatial coordinates of involute by MATLAB programming and generate accurate spherical involute of tooth profile, Only in this way can the accurate three-dimensional model of spur bevel gear be established.
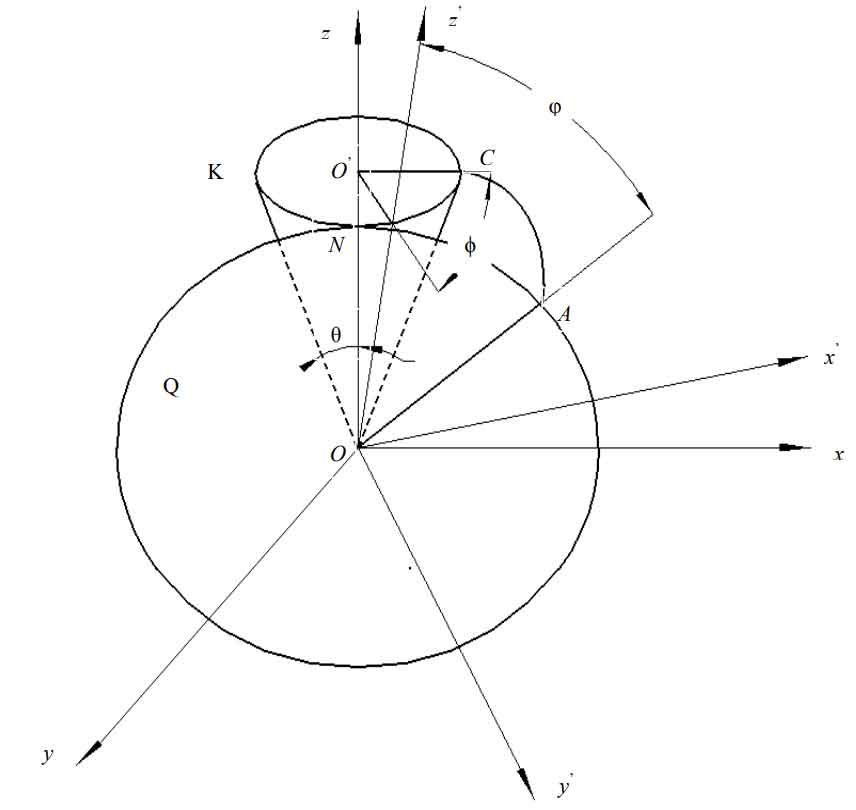
As shown in Figure, the formation process of involute is shown. The plane Q tangent to the base cone rolls along the base cone around the center O. at this time, the trajectory of the spatial motion of the straight line OA passing through the center of the circle on plane q is the conical involute surface. When a sphere with any radius taking the apex of the cone as the center intersects with the conical involute surface, the spatial spherical involute can be obtained (such as the arc Ca in Figure). If the radius of a sphere centered on the apex of a cone reaches infinity, the intersection of the sphere and the conical involute will be a plane involute.
The spatial involute equation of spur bevel gear is as follows: