Gear backlash is the amount of circumferential shaking of another gear when one gear is fixed, which is calculated by the arc length on the graduation circle. It is to ensure the formation of a normal lubricating oil film between the tooth surfaces and prevent the gear teeth from being stuck due to the expansion deformation caused by the increase of the working temperature of the gear. Therefore, gear backlash is inevitable.
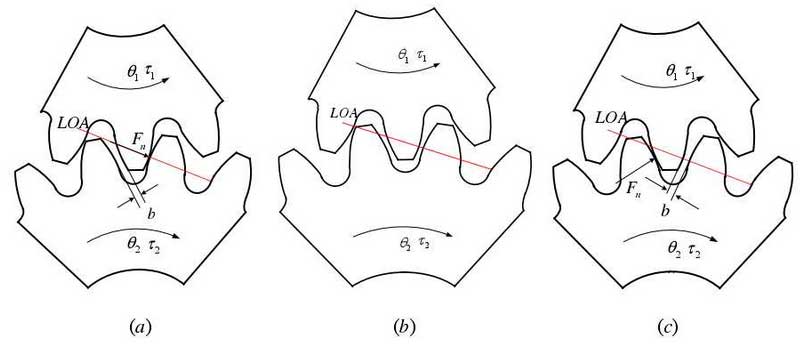
On the one hand, the negative effect of backlash makes the backlash of gear transmission increase, which affects the transmission accuracy. On the other hand, it mainly comes from the impact of dynamic vibration. When the driving speed is not stable or the driving torque direction and amplitude change, the reciprocating impact of active and passive engagement tooth surface produces obvious noise, and it may also increase the contact stress to accelerate the wear. Three meshing states with gear backlash are described in Figure 1. The backlash is B, the rotation angle of the driving gear is θ 1, the rotation speed of the passive gear is θ 2, the moment acting on the gear is τ 1, τ 2, and the radius of the base circle is R1, R2, respectively.
(a) When the driving gear drives smoothly, that is, there is no speed fluctuation, and the driving tooth surface and the driven tooth surface always maintain contact and transmission torque. here
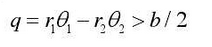
The dynamic equation is as follows:
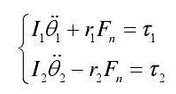
Where k is the meshing stiffness:
(b) When the driving gear fluctuates, the driving gear and the driven gear lose teeth, and there is no torque transfer (0nf =) f 0nf =) between the gears. here
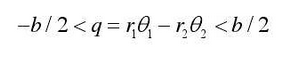
The dynamic equation is as follows:
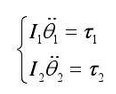
(c) The passive gear is ahead of the driving gear. At the moment, the tooth back contacts, and the passive wheel drives the driving gear in reverse. here
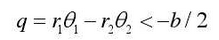
The dynamic equation is as follows:
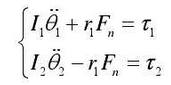
In this case, K is the meshing stiffness.
Without meshing damping, the meshing force of gear surface with backlash is expressed as follows:
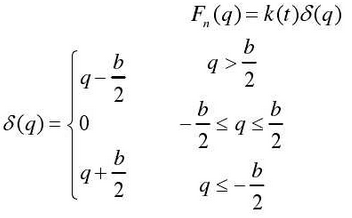
The existence of gear backlash increases the difficulty of numerical solution. For example, the Runge Kutta method with 4-5 order variable step size is used to solve the problem. When approaching the singular point, the integration step size will decrease continuously, resulting in the phenomenon of non convergence. In order to overcome this problem, it is necessary to smooth the discontinuous or segmented functions in the gap function.
Here, the symbolic function SGN (x) is introduced as follows, which is a continuous piecewise function:
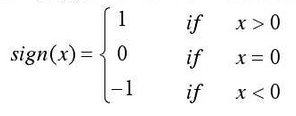
The sign function is smoothed by arctangent function:
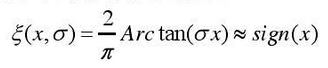
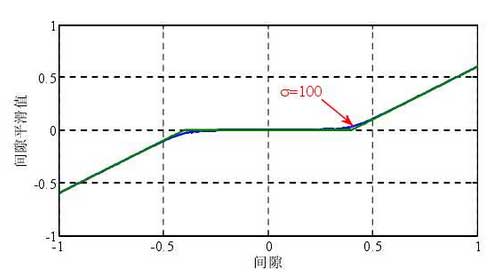
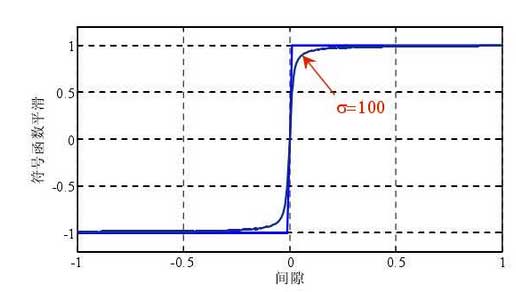
The two functions are basically the same except at 0. The smooth function can be differentiated at 0, and its smoothness is controlled by the parameter σ, but the sign function cannot be differentiated at 0. Figure 5.3 shows the comparison after σ = 100 smoothing.
For the processing of all the gap subsection functions, firstly, it is written in the form of symbol function, then it is smoothed by using smoothing function, and its smoothness is controlled by parameter σ.
Smooth the meshing force of tooth surface with clearance, and the formula can be transformed into:
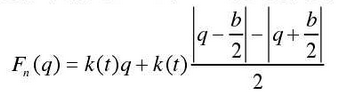
Represented by symbolic function:
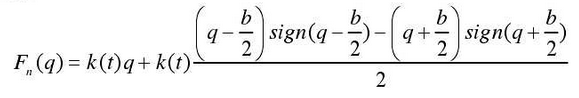
After smoothing, it is expressed as:
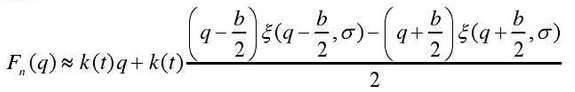
Figure shows the smoothing result with a gap of 0.8.