The forming principle diagram of cylindrical gear tooth surface with circular arc tooth line processed by parallel linkage mechanism is established. On the forming principle diagram, the gear tooth surface ∑ is formed by scanning the involute tooth profile th of the gear end face along the tooth direction line of the base cylinder, and the gear tooth surface equation is also established.
In the coordinate system S1 (o1-x1y1z1), the plane of x1o1y1 is the middle section of the base cylinder, and Z1 axis is on the axis line of the base cylinder; the ZH of the coordinate system sh (oh xhyhzh) is in the same direction with the axis Z1, the distance between the xhohyh plane and the x1o1y1 plane is h, and the angle between the XH axis and the starting point of the involute base cylinder in the xhohyh plane and the Y1 axis is β (called position angle), and the size of the position angle β is β = (RT – R2T- h2) /R1。 Where: R1 is the radius of the dividing circle of the gear; RT is the radius of the tooth line.
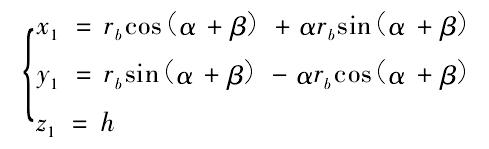
The tooth surface equation is as follows:
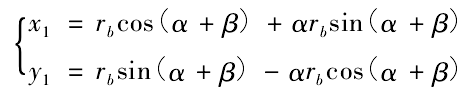
Where: B – tooth width; Rb – radius of base cylinder. It can be seen from the tooth surface equation that z-coordinate of cylindrical gear with circular tooth profile machined by parallel linkage mechanism is an independent parameter
If we want to express the other side of the tooth surface ∑ ‘or tooth profile, we only need to select the coordinate system and repeat the derivation process of the tooth surface equation ∑ or tooth profile.
