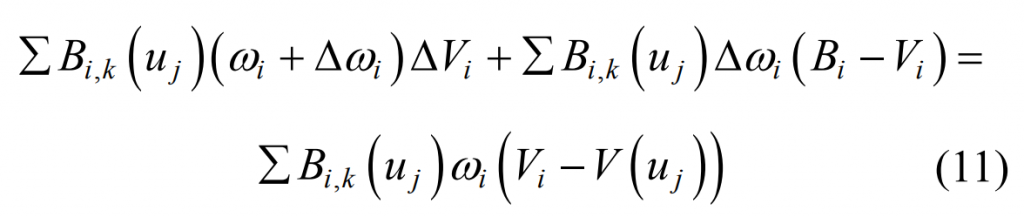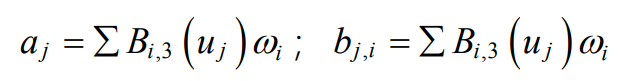The traditional NURBS surface interpolation algorithm interpolates the curve first and then fairs the curve. The defect of this method is to change the control vertices of NURBS surface to ensure the smoothness of the surface and “ignore” some measurement points. This difference method which only changes the control vertices is difficult to ensure the accuracy and has great limitations when constructing the real tooth surface of hypoid gear with tooth surface wear.
Based on the proposed hypoid gear tooth surface interpolation algorithm based on area weight method, considering the compensation of construction error, and combined with the non feature-based discrete data block technology, an improved NURBS surface local interpolation algorithm is proposed. When the measured data points are limited, how to determine the tooth surface data of hypoid gear at the interpolation position and the adjustment amount of weight factor at the corresponding control vertex are the two difficulties of the interpolation algorithm.
According to the non feature-based discrete data blocking technology, the mesh area of hypoid gear tooth surface that fails to meet the formula is extracted as the interpolation object.
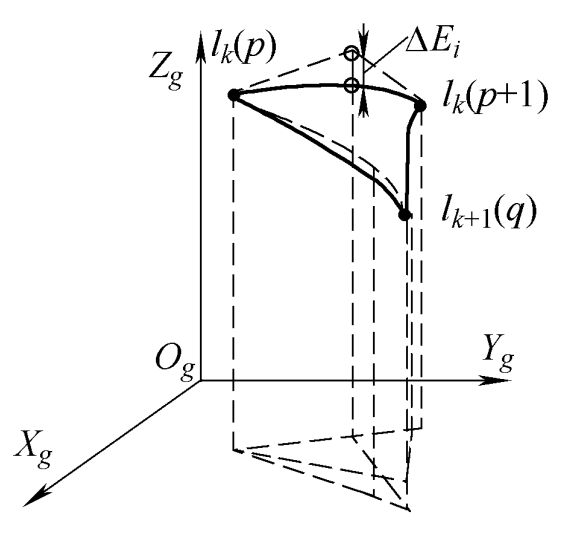
Through the triangular region numerical interpolation algorithm, the tooth surface data in the non measurement region of the tooth surface of hypoid gear is obtained, which is used as the control vertex VI of the interpolation curve p ‘(U) and the corresponding weight factor ω i. Is the construction curve p ‘(U) interpolated to all discrete data points obtained by interpolation algorithm, and the deviation between the control vertex VI and the p’ (U) value point of the interpolation curve is Δ EI, as shown in Figure 1.
Where, VI is the control vertex of the curve; Δ VI is the change amount of the control vertex of the curve; ω I is the weight factor of VI; Δω I is the weight factor change of VI; Bi, K, is a B-spline basis function of degree K along the U direction.
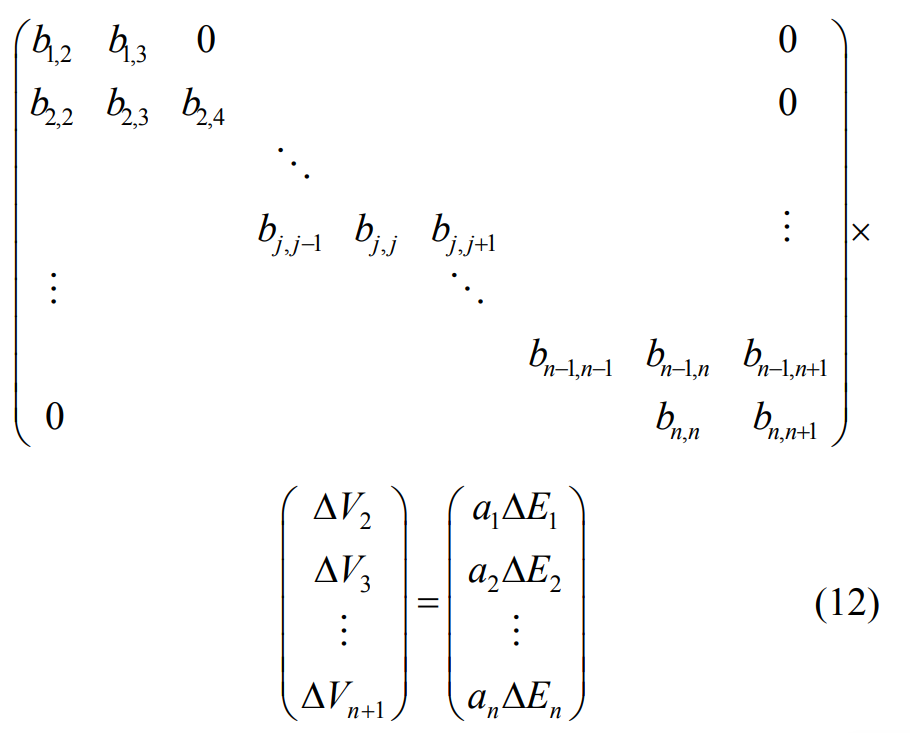
In order to realize the construction error of NURBS surface Δ EI compensation, so that the interpolation curve passes through the interpolated data points, the position of the control vertex needs to be adjusted. The formula is applied to the cubic NURBS surface interpolation algorithm to adjust the amount for the control vertex( Δω I = 0) the solution formula is:
Where:
Adjustment amount of weight factor corresponding to control vertex( Δ VI = 0), the solution formula is: