In order to study the influence of the mean value of the time-varying meshing stiffness on the vibration characteristics of the system, based on the time-varying meshing stiffness curve calculated previously, five different mean values of time-varying meshing stiffness (0.6 times, 0.8 times, 1.0 times, 1.2 times and 1.4 times) were taken as the system excitation, and the relative vibration acceleration in the direction of the meshing line of the gear end face was obtained. The results are shown in Fig. 2 As shown in Fig.

In Fig. 2, when the amplitude of time-varying meshing stiffness is constant, the vibration response of the system with different mean value of time-varying meshing stiffness is significantly different. In the non resonance region, the root mean square value of the relative vibration acceleration along the meshing line decreases with the increase of the average meshing stiffness. It can be seen that the resonance speed of the system has also changed. The resonance speed of the gear pair increases with the increase of the mean value of the time-varying meshing stiffness of the gear pair. The numerical variation law of the resonance speed conforms to the formula of the natural frequency of the system s / M (/ degree speed plus dynamic vibration direction square meshing 2) as shown in the formula

Further analysis shows that the decrease of the mean meshing stiffness makes the change rate of the root mean square value of the relative vibration acceleration near the resonance speed of the system larger than that of the rotation speed, which leads to the deterioration of the stability of the gear vibration when the gear speed reaches the resonance speed of the system.

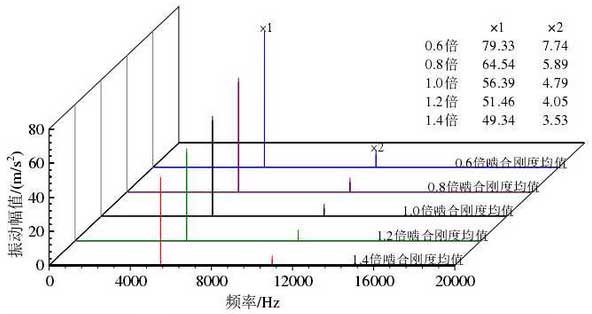
Fig. 3 and Fig. 4 are the time domain diagrams of the vibration along the meshing line under five different meshing stiffness mean values at 6000rpm and 15000rpm respectively, and the frequency domain diagrams are shown in Fig. 4 and Fig. 6.

It can be seen from Fig. 3 that the larger the mean value of time-varying meshing stiffness is, the smaller the fluctuation of relative vibration acceleration is. Fig. 4 shows that the amplitude of vibration frequency response decreases with the increase of mean value of time-varying meshing stiffness. According to the specific amplitude of vibration acceleration in Fig. 3 and Fig. 4, the vibration acceleration amplitude of the system under 0.6 times of the mean meshing stiffness is about 3 times of that under 1.0 times of the mean meshing stiffness, and the amplitude of the vibration acceleration of the system at 1.0 times of the mean value of the meshing stiffness is about 2 times that of the 1.4 times of the average meshing stiffness.

This is due to the fact that 6000rpm is close to the resonance speed under the mean values of these meshing stiffness, so the average meshing stiffness has a significant impact on the vibration response. That is to say, near the resonance speed, the influence of the mean value of time-varying meshing stiffness on the vibration of the system is more significant. S / M (/ degree speed acceleration vibration direction square line engagement 2)