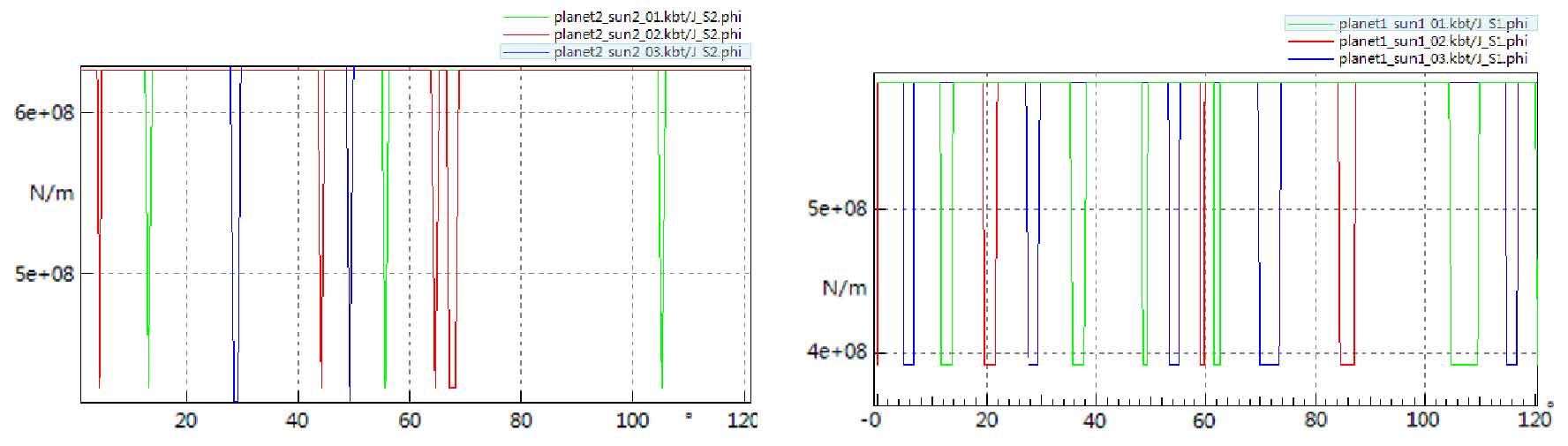
There are three cases for the influence of tooth surface contact phase angle on parameter excitation intensity: the first case, when the arrangement of all planetary gears is symmetrical (120 ° away from each other). The number of teeth of the large sun gear S2 is 38, the number of teeth of the small sun gear S1 is 28, and the number of teeth of the ring gear is 89. Because the number of central theoretical teeth is not a multiple of 3, that is, the triple symmetry is destroyed, and the stiffness curves of the contact of the three planetary teeth are not synchronized. It means that different vibration modes will be generated, as shown in Figure 1 (a) (b).
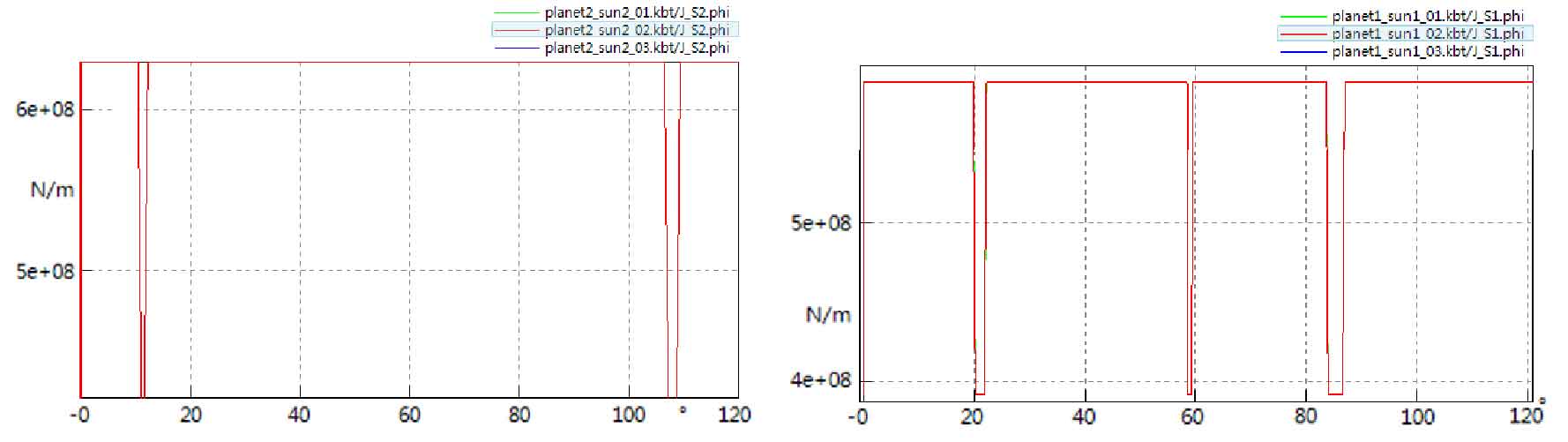
In the second case, ensure that the center distance of the composite planetary row mechanism remains unchanged. When the number of teeth of the large sun gear S2 is 39, the number of teeth of the small sun gear S1 is 27 and the number of teeth of the ring gear is 90. When the arrangement of all planetary gears is symmetrical, the stiffness curves of all minimum and maximum values are consistent. The superposition with the oscillation amplitude of meshing stiffness will cause a strong parametric excitation, as shown in Fig. 2 (a) (b).
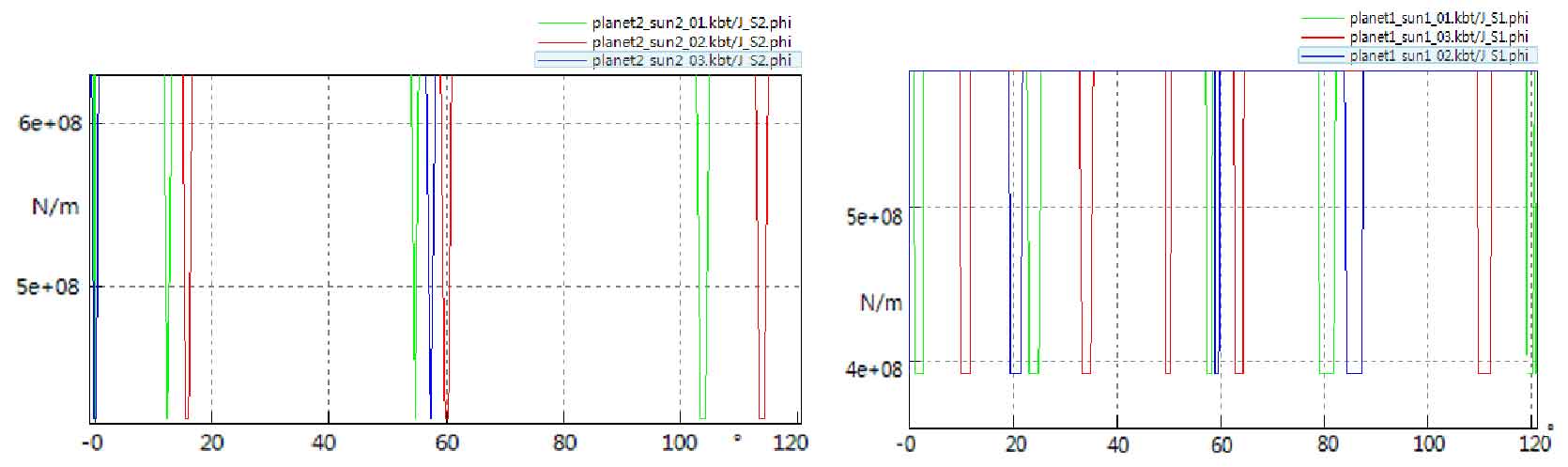
In addition, the influence of the third case on the relative position of the tooth surface contact point is studied. In this case, the position of the planetary gear shaft is asymmetric. In general, the offset is possible. When the number of teeth of the large sun gear is 38, the number of teeth of the small sun gear is 28 and the number of teeth of the ring gear is 89, the minimum offset angle of the asteroid gear meshed with the large sun gear is δ Min = 360 / (ZS2 + Zr) = 2.83, the minimum offset angle of the large planetary gear meshed by the small sun gear is δ min=360/(zs1+zr)=3.07。 Therefore, when the planetary gear is not designed into three 120 ° same angles, but γ p21=114.34°, γ p22=122.83°, γ p23=122.83°, γ p11=113.84°, γ p12=123.08°, γ P13 = 123.08 °, so the vibration excitation in the tangential direction will be reduced and will no longer be balanced in the radial direction due to asymmetry, as shown in Fig. 3 (a) (b).