1.Establish involute tooth profile curve equation
The theoretical tooth profile curve of spur bevel gear is spherical involute. Because the spherical involute cannot be expanded into a plane, it brings great difficulties to the three-dimensional modeling of bevel gear. Based on the theory of back cone, the equation of involute profile curve of bevel gear is established.
A complete gear tooth profile should have four part curves to form the tooth root arc curve, involute tooth profile curve, tooth top arc curve and the connection curve connecting the involute tooth profile and tooth root arc. According to the size relationship between the base circle and the tooth root circle, the tooth profile curve equation of involute gear is given in two cases. The connecting curve between the tooth root arc of bevel gear and the involute tooth profile is specified as follows: when the radius of the base circle is greater than the radius of the tooth root circle, the straight line segment of the involute base circle radial direction is used as the connecting curve; When the radius of the base circle is less than or equal to the radius of the tooth root circle of the bevel gear, the involute tooth profile is directly connected with the tooth root arc, and there is no connection curve.
(1) The radius of the base circle is greater than the radius of the tooth root
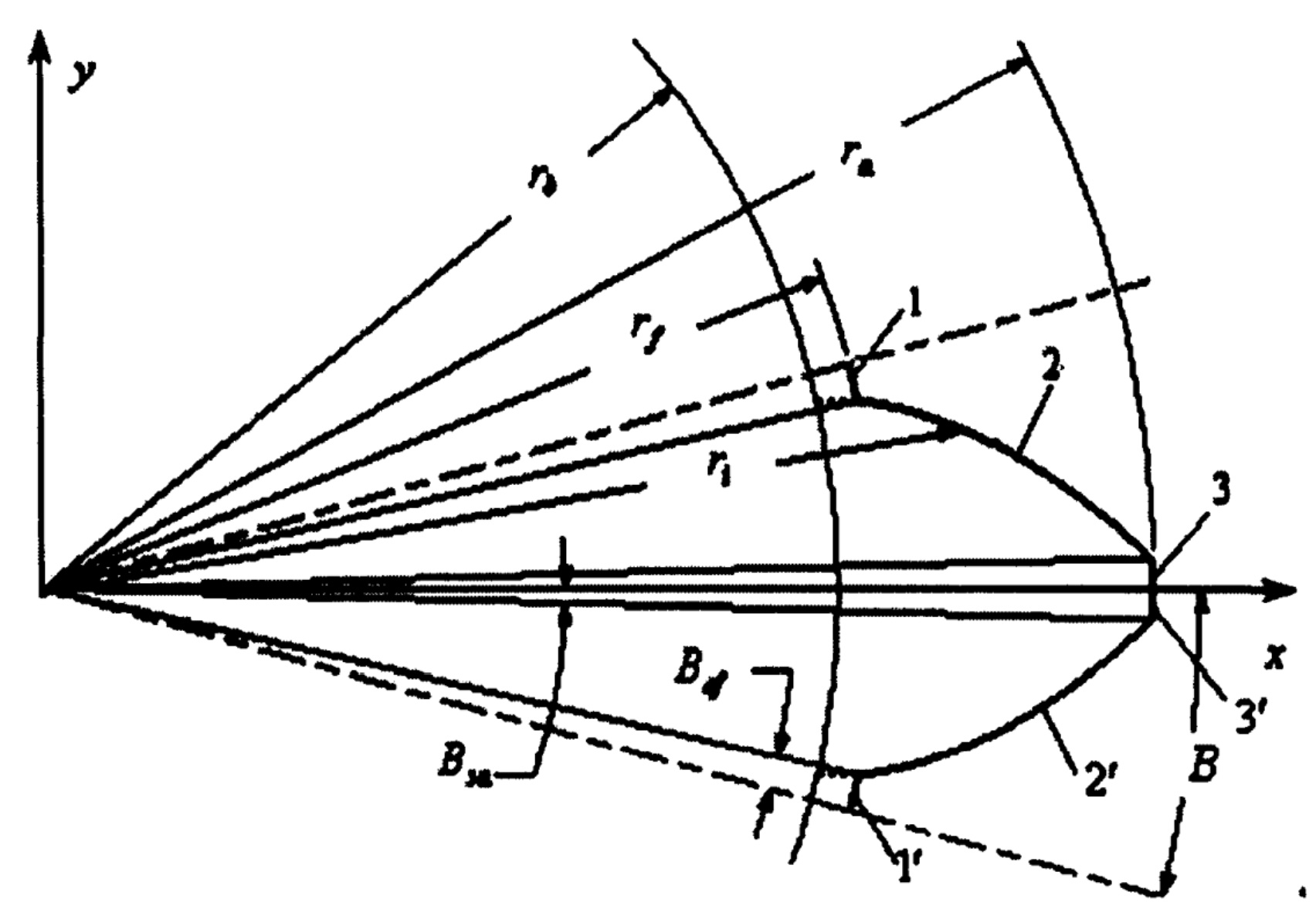
When the radius of the base circle is greater than the radius of the root circle of the bevel gear, the tooth profile consists of four curve segments, as shown in Figure 1. The four curve segments above the x-axis are named curve 1, curve 2, curve 3 and curve 4 respectively. Accordingly, the four curve segments below the x-axis are named curve 1′, curve 2′, curve 3 ‘and curve 4’ respectively.
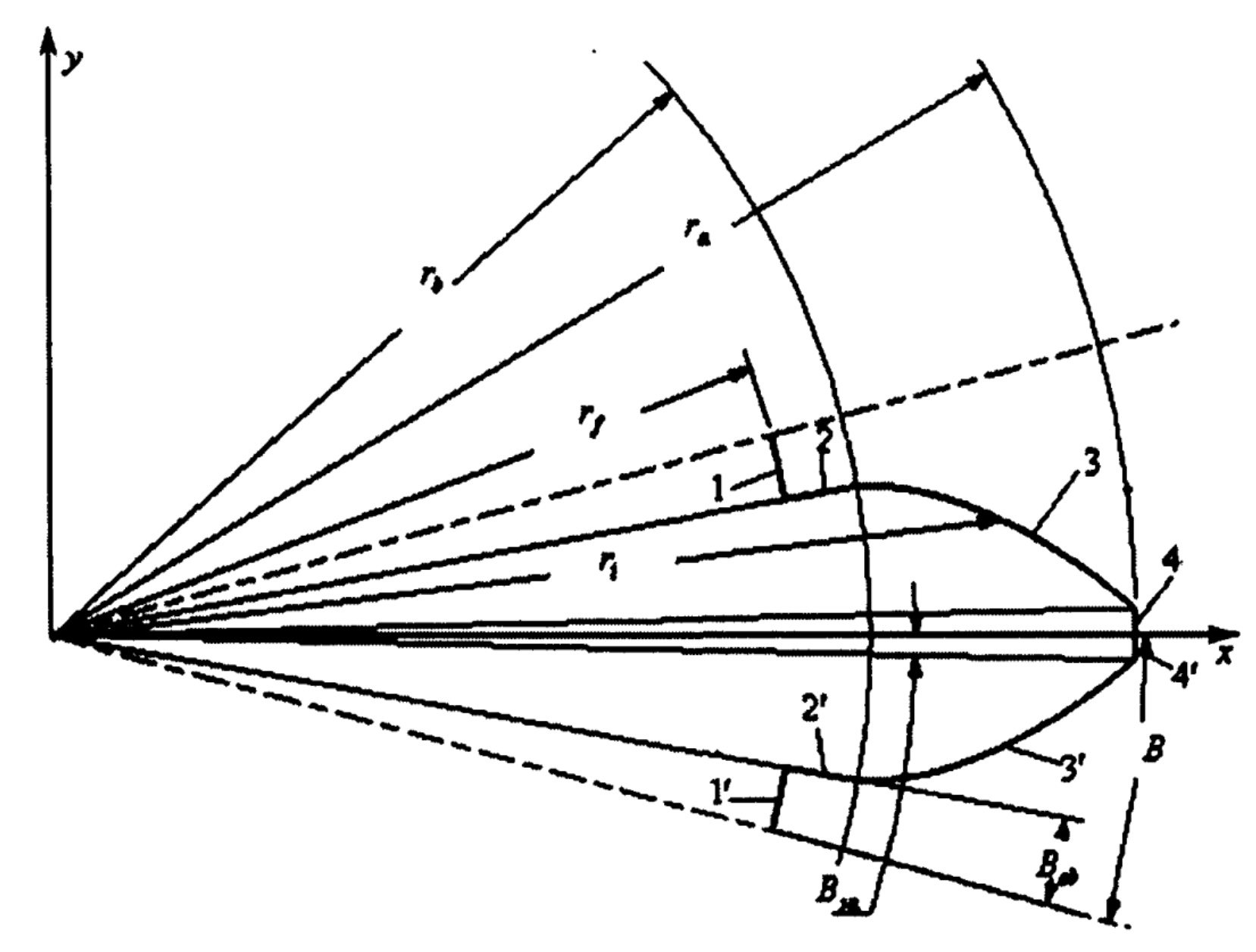
The critical radii RF, Rb, R of these four curves α, Critical angle B, beb, BSB, BS α And relevant parameters RI α i、 β The calculation formula of I is shown in the attached table. According to the properties of involute tooth profile and the geometric relationship in Figure 1, the involute tooth profile curve equation can be obtained.
Equation of curve 1 (tooth root arc curve):
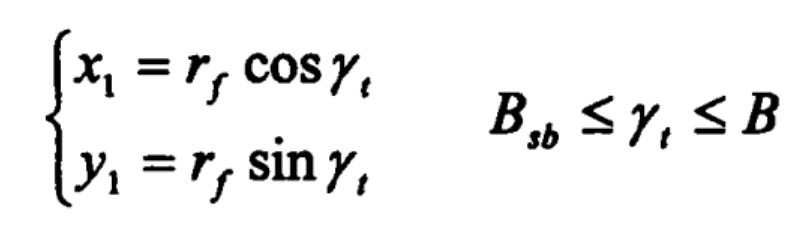
Where
γ T – parameter angle;
RF – radius of tooth root circle of bevel gear;
B – half of the center angle of a complete gear tooth;
BSB – half angle of base circular gear tooth.
Equation for curve 2 (connecting segment curve):
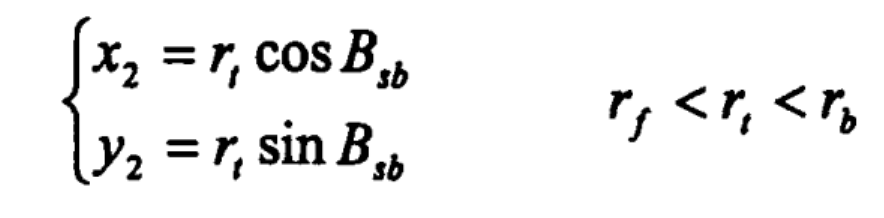
Where
RT – parameter;
RB – radius of base circle.
Equation for curve 3 (involute profile curve):
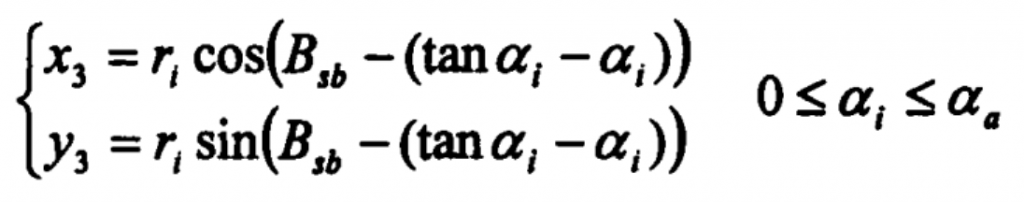
Where
RI – radial diameter of any point on the tooth profile of involute bevel gear;
α I – pressure angle at any point on the tooth profile of involute bevel gear.
Equation of curve 4 (Addendum arc curve):
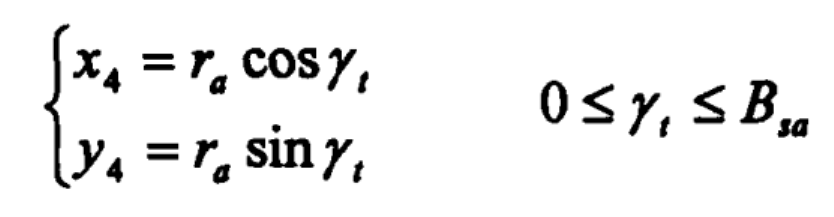
Where
γ T – parameter angle
r α— Radius of addendum circle of bevel gear
Bs α — Half angle of circular tooth at the top of bevel gear.
Accordingly, the equations of the four curves below the x-axis can be obtained.
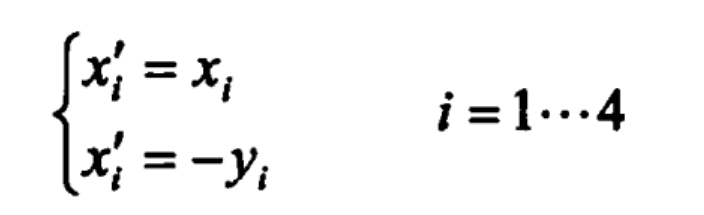
(2).The radius of the base circle is less than or equal to the radius of the tooth root group
When the radius of the base circle is less than or equal to the radius of the root circle of the bevel gear, the tooth profile consists of three curve segments, as shown in Figure 2. The three curve segments above the x-axis are named curve 1, curve 2 and curve 3 respectively, and the three curve segments below the corresponding X-axis are named curve 1′, curve 2′ and curve 3 ‘respectively.
The critical radii RF, R of these three curve segments α , Critical angle B, BS α、 Bef, BSF and related parameters RI α i、 β The calculation formula of I is shown in the attached table. According to the tooth profile properties of involute bevel gear and the geometric relationship in Figure 2, the tooth profile curve equation of involute bevel gear can be obtained.
Fig. 2 Schematic diagram of derivation of tooth profile curve equation when the radius of base circle is less than or equal to the radius of bevel gear tooth root circle.
Equation of curve 1 (tooth root arc curve):
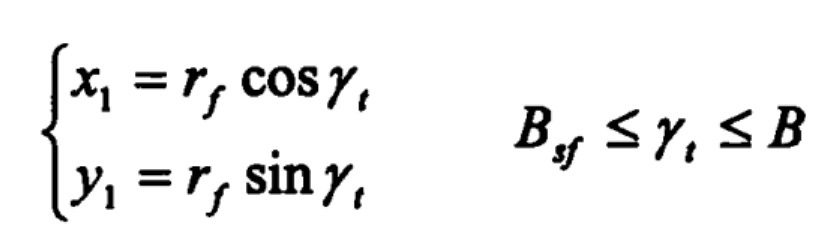
Where
γ T – parameter angle
BSF – half angle of circular tooth at the root of bevel gear.
Equation for curve 2 (involute profile curve):
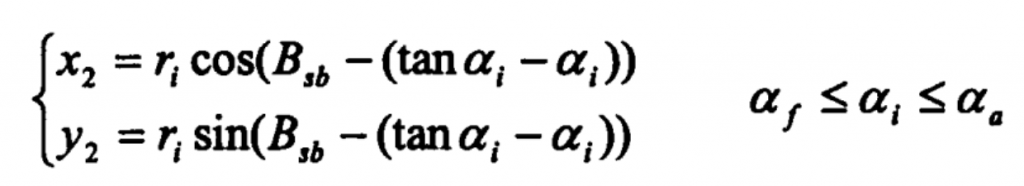
Where
α 1 – pressure angle at any point on the tooth profile of involute bevel gear.
Equation of curve 3 (Addendum arc curve):
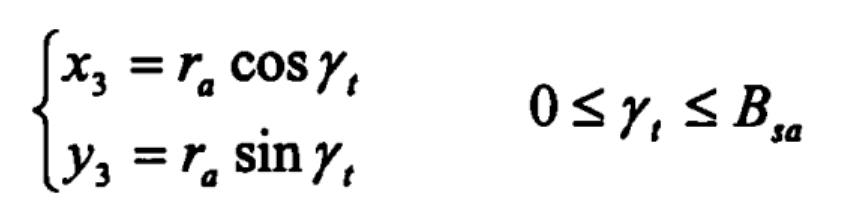
Where
γ T – parameter angle;
Accordingly, the equations of the four curves below the x-axis can be obtained:
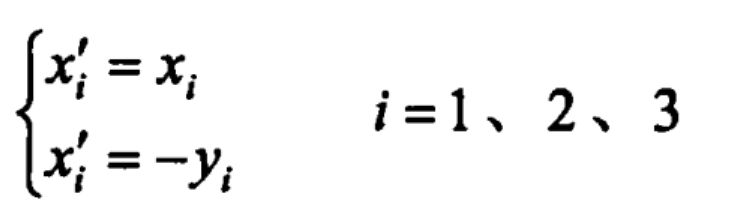
2.Application examples
The given involute tooth curve depends on the basic tooth profile parameters of the bevel gear. Once the basic tooth profile parameters of the bevel gear are determined, the tooth profile diagram of the bevel gear can be drawn conveniently and accurately by using the curve command in UG according to the formula. Fig. 3 is the big end tooth profile of bevel gear obtained in UG.

