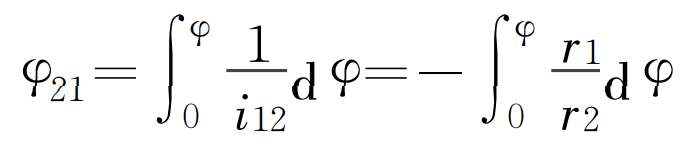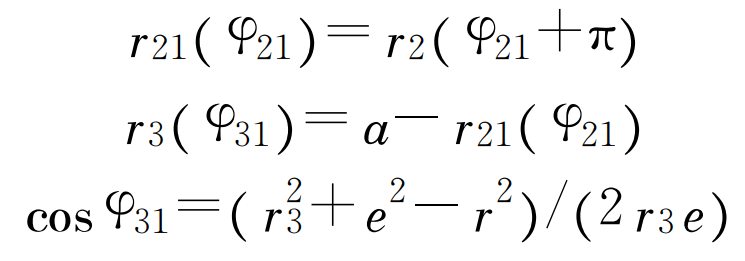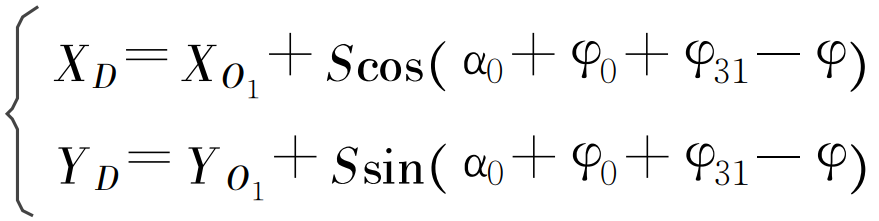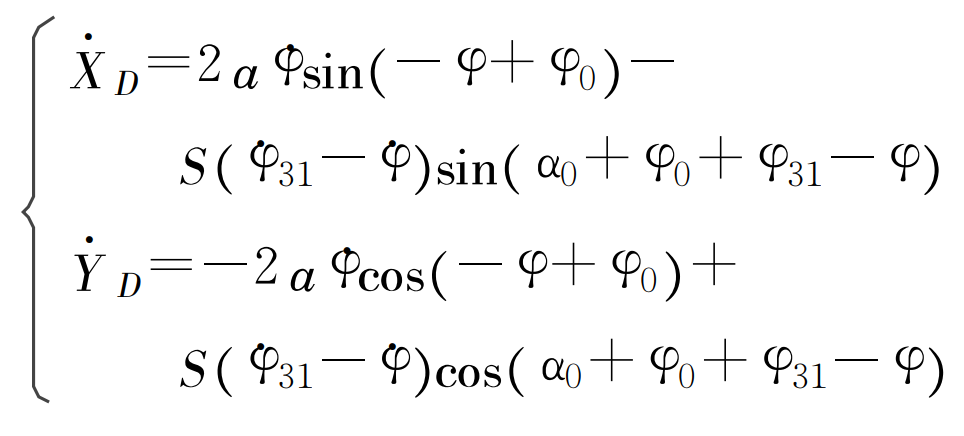1. Analysis of transmission angular displacement of eccentric gear and conjugate noncircular gear
The initial position of the five gear drives is shown in Figure 1a. Let the direction axis oo1 be the initial rotation side of the planet carrier, and the included angle between the planet carrier 3 and the x-axis at the initial position is φ 0 The angular displacement of planet carrier 3 from the initial position is φ, Its counterclockwise rotation relative to the initial edge is positive and clockwise rotation is negative.
The planet carrier rotates clockwise around point O from its initial position φ When, gear 5 turns clockwise with respect to planetary carrier 3 φ 21, as shown in Figure 1b. I12 = – R2 / R1, calculated by numerical integration φ 21, get:
When φ When it is 0 ~ – 2 π, φ 21 is also 0 ~ – 2 π.
As can be seen from figure 1A:
When the planet carrier rotates clockwise φ When, planetary gear 6 rotates counterclockwise with respect to the planet carrier φ 31。 Therefore, when φ When it is 0 ~ – 2 π, φ 31 is 0 ~ 2 π.
2. Displacement model
According to the rectangular coordinate system xoy shown in Fig. 1, the displacement of the planetary gear rotation center O1 is:
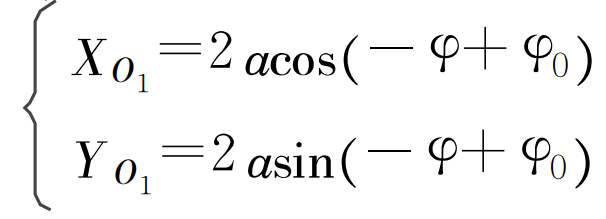
The relative movement of point D of seedling needle tip (equivalent to when the machine is stationary) displacement is:
Where:
α 0 – angular displacement between the connecting line between the planetary gear center O1 and the seedling needle tip D and the planetary carrier om1 at the initial position;
S – distance between planetary gear rotation center O1 and seedling needle tip D.
3. Needle tip velocity model of seedling
When planetary carrier 3 rotates at a uniform speed, its angular velocity increases φ·=ω Is a constant. Angular velocity of the intermediate gears (non-circular gears 2 and 5) relative to the planet carrier ω 21= φ· 21. The relative motion speed of point D of seedling needle tip is: