The optimization problem in forging process includes two aspects: first, analyze the optimization design problem and establish the corresponding mathematical model, including selecting design variables, listing objective functions, giving constraints, etc. at the same time, considering the finite element analysis of forging process, through the analysis of given process parameters (such as material parameters, friction coefficient, die shape, etc.) The forging process of metal gear blank is simulated by finite element method, and the results of stress, strain and temperature distribution in the forming process and the maximum pressure borne by the die are obtained; The second is the optimization method itself, that is, what kind of optimization algorithm is used to optimize the given objective function (such as the minimum material damage value, uniform tissue distribution, minimum material consumption, minimum metal deformation force, etc.) by using the results of finite element analysis, so as to obtain the ideal forging.
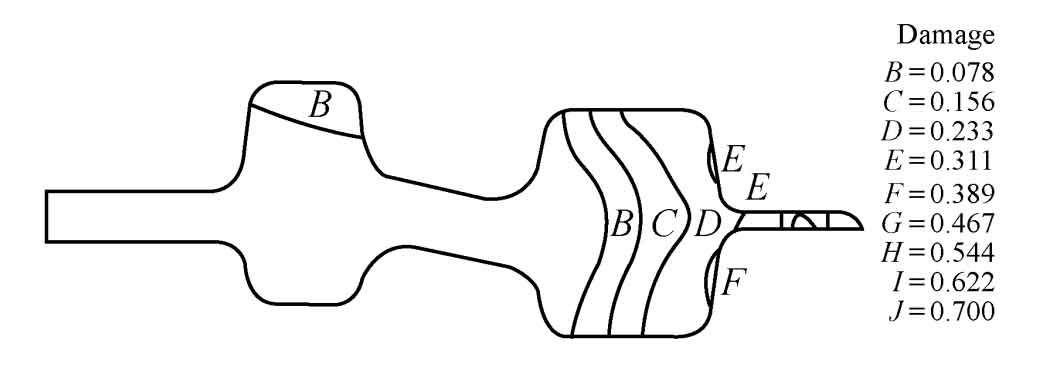
The hot forging process of the gear blank is analyzed with the commercial finite element software DEFORM-2D. The hot forging diagram of the gear is shown in Figure 1. The forging gear blank is a circular bar material, which directly enters the final forging groove for final forging after upsetting by the die upsetting table. The shape of the gear blank after upsetting has an impact on the final forging formability of the part (such as the damage value of the material) It has a very important influence. Through the combination of design optimization method and finite element numerical simulation technology, an optimal height diameter ratio of gear blank can be found to minimize the material damage value of final forging. Because the part belongs to axisymmetric plane problem, take 1 / 2 of the part for finite element calculation. The corresponding relationship between blank and upper and lower dies is shown in Figure 2.
According to the corresponding damage model, when the damage value of the deformed body reaches the critical damage value of the material, the material breaks; When it is less than the critical value, the damage value reflects the size of the material fracture trend. The material damage value at a certain point of the deformed body is generally the integral of the strain at this point, and the critical damage value of the material is obtained by experiments. In DEFORM software, many material damage models are provided, and Cockroft & Latham model is selected to determine the damage value of the material.
Of which: σ Is equivalent stress; σ* Is the maximum stress, when the maximum principal stress σ When 1 ≥ 0, σ=σ 1, σ When 1 < 0, σ= 0 ε F is the strain when the material breaks; ε Is the equivalent strain.
The objective function is an analytical expression that represents a certain performance index pursued by the design with design variables. In this paper, it is considered to select appropriate process parameters to minimize the internal damage value of the forging after deformation. Therefore, the maximum damage value D max of all elements of the forging (excluding the flash part) is used as the index to measure the deformation damage of the forging, The objective function for controlling the internal damage value of forgings is defined as follows:
When D Max is less than the critical failure value of the material, the smaller D Max is, the better the performance of the final formed part actually obtained and the less the possibility of cracking. Therefore, f (x) is the deformation damage index or measure. Taking the initial height diameter ratio H0 / d0 of the part gear blank as the design variable, Through the finite element numerical simulation and parameter optimization of gear blank forgings, the optimal initial height diameter ratio H0 / d0 can be obtained.
On the other hand, in addition to the quality requirements, the ideal forging should also meet the accurate shape required by the design. Since the shape of the forging is guaranteed by the die cavity, this requires the material to completely fill the die cavity. In the process of forging hot forging, if the selection of process parameters is unreasonable, the metal may not completely fill the die cavity. Therefore, In the process of optimization design, it should be considered that the metal completely fills the cavity as the constraint condition. The index characterizing this condition is the percentage of the volume difference between the ideal forging and the actual forging in the volume of the ideal forging, which is defined as:
Where: V I is the volume of ideal forging; V s is the volume of the actual forging. The value of G is close to zero, indicating that the metal is completely filled with the cavity. The mathematical model for the optimization of process parameters in the hot forging process of gear blank is as follows:
Of which: ε Is a number close to zero; X min and X Max are the value range of H0 / d0 respectively.
Using the above mathematical model and optimization algorithm – reduced descent gradient method, the process parameters of gear blank hot forging process shown in Figure 1 are designed and optimized. It is assumed that the material is an ideal viscoplastic material and the whole forming process is a non isothermal process. The gear blank material is 40Cr and the forging temperature is 1000 ° C, The die is preheated to 300 ° C. the friction coefficient between the gear blank and the die is 0.3, the heat transfer coefficient is 5W / (M2 · K), and the downward speed of the upper die is 50mm / s. The value range of H0 / d0 of the part gear blank is 0.15 ~ 1.3. Fig. 3 shows the variation trend of the objective function with the number of iterations, Fig. 4 shows the variation trend of design variables with the number of iterations. The optimized finite element simulation results are shown in Fig. 5. It can be seen from Fig. 3 and 4 that after 21 iterations, the value of objective function decreases from the highest point of 0.94 to 0.33, and finally converges near 0.35, and the optimal H0 / d0 = 0.35. The value of objective function decreases by 65.35%, with a large decrease, and the optimization effect is obvious.