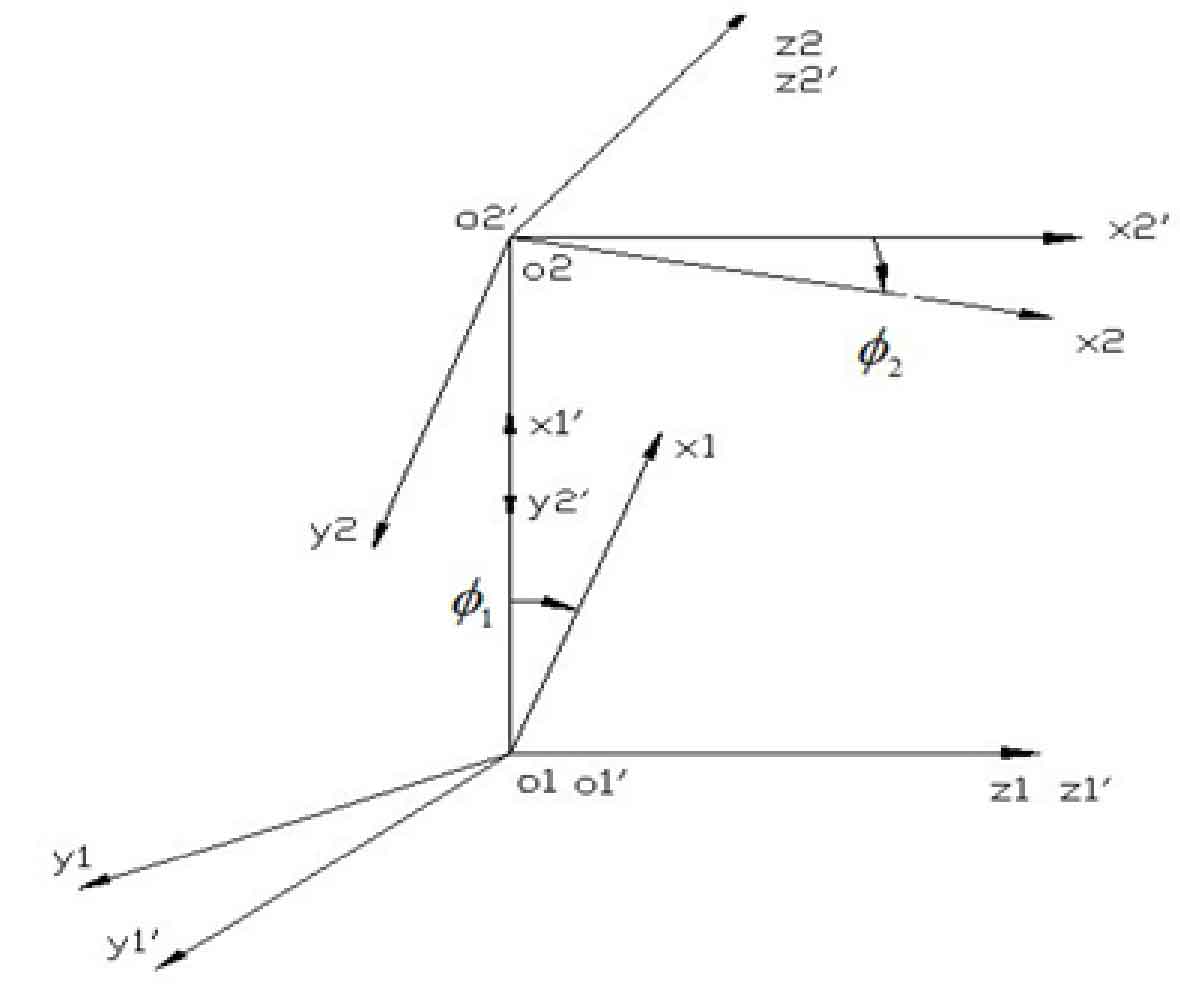
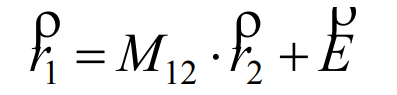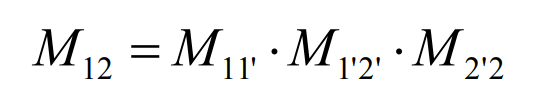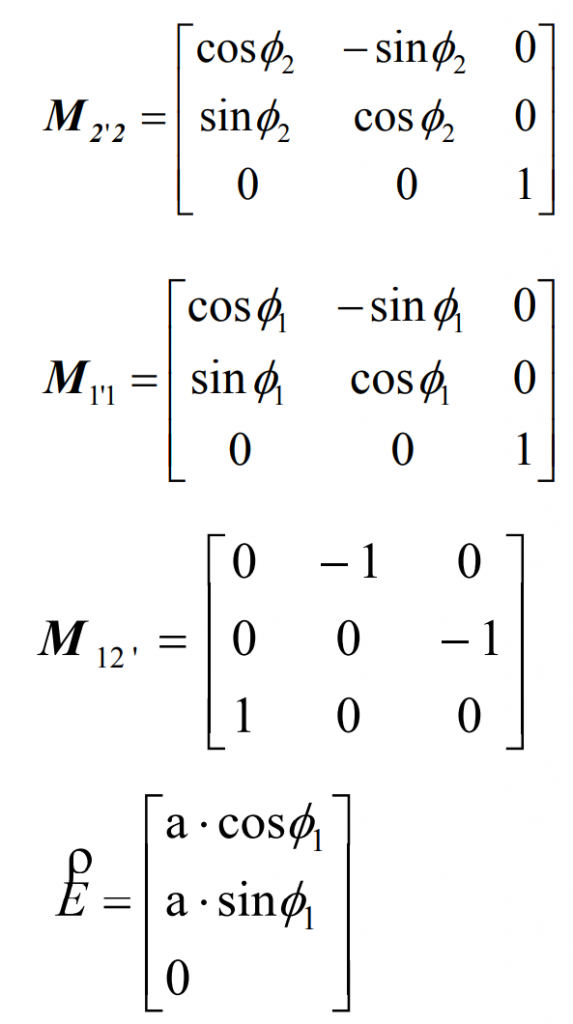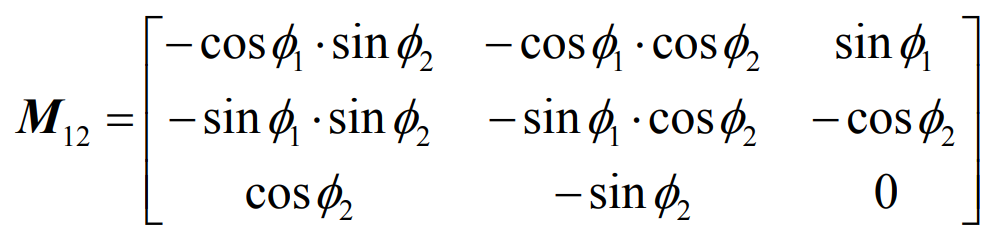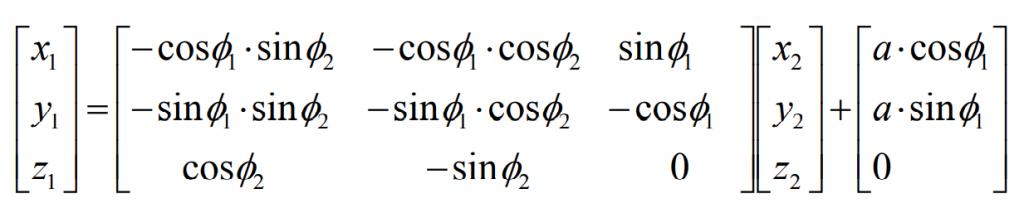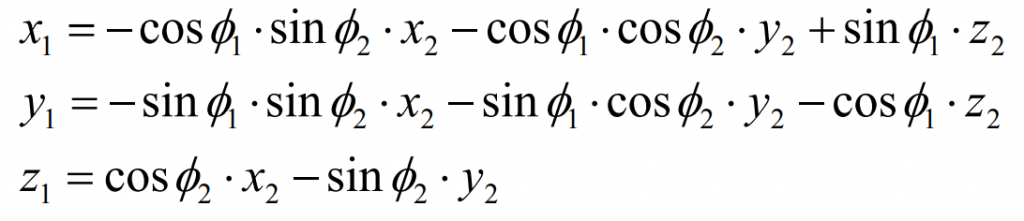The hypoid gear pinion with small number of teeth and high speed uses the principle of envelope method to envelope the tooth surface of the small gear with the large tooth surface of hypoid gear pinion. According to this production principle, the coordinate system shown in the figure is established to describe the envelope process of hypoid gear pinion:
S2 ´ = [O2 ´; x2 ´, Y2 ´, Z2 ´] is the coordinate system of hypoid gear wheel, O2 ´ is the center of big wheel, Z2 ´ and ω 2 coincidence, Y2 ´ refers to the direction of the common vertical line between the small wheel axis and the large wheel axis;
S2 = [O2; X2, Y2, Z2] is the active coordinate system of hypoid gear wheel, O2 coincides with O2 ‘, Z2 coincides with Z2’, S2 is in S2 ‘, and the angle is Φ 2 means;
S1 ´ = [O1 ´; x1 ´, Y1 ´, Z1 ´] is the coordinate system of hypoid gear pinion, O1 ´ is the center of pinion, Z1 ´ and ω 1. Overlap, x1 ´ along the direction of the common vertical line;
S1 = [O1; x1, Y1, Z1] is the active coordinate system of hypoid gear pinion, O1 coincides with O1 ‘, Z1 coincides with Z1’, S1 is in S1 ‘, and the angle is Φ 1 indicates.
In the process of envelope, Φ 1=i21. Φ 2; I21 is the transmission ratio of hypoid gear wheel.
After the above coordinate system is established, the expression of tooth surface equation and unit normal vector equation of hypoid gear pinion in hypoid gear pinion coordinate system S1 is deduced below.
In order to obtain the tooth surface equation of hypoid gear wheel, the tooth surface of tool hypoid gear wheel is Σ 2 the vector equation in the coordinate system S2 is transformed from the coordinate system S2 to the coordinate system S1, so the following formula holds:
Coordinate transformation matrix:
Substituting the formula, we can get:
Substitute the formula to obtain:
Expand the right end to obtain:
Where, Φ 2=i12 Φ 1. Matrix M2 ‘2 is the transformation matrix from coordinate system S2 to S2’, M1 ‘1 is the transformation matrix from coordinate system S1 to S1’, M12 ‘is the transformation matrix from coordinate system S2’ to S2, and E is the column matrix of the radial vector of the origin O2 of S2 in S1.