In the optimization design of bevel gear transmission mechanism, the minimum volume sum of bevel gear pair is taken as the design objective.

As shown in Figure 1, the main structural dimensions of bevel gear pair with 90 ° intersection angle include indexing circle diameter D, bevel gear pair pitch R, bevel gear width b, indexing cone angle δ, etc.

The volume and V of bevel gear pair are:

Where: Z1 and Z2 are the number of teeth of big and small bevel gears respectively; m is the large end modulus of bevel gear pair; R is the pitch of bevel gear pair; B is the width of bevel gear; ψ R is the tooth width factor; δ 1 and δ 2 are the indexing taper angle of big and small bevel gears respectively.

It can be seen from the formula that the parameters affecting the volume sum of bevel gear pair are the number of teeth Z1 of small bevel gear, the modulus m of large end of bevel gear pair, and the tooth width factor ψ R. therefore, the design variable x can be set as:

The contact strength condition of tooth surface is as follows

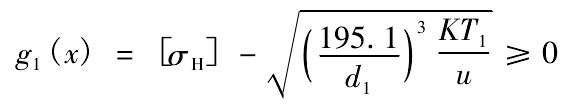
Where: [σ H] is the allowable contact stress of the tooth surface of the bevel gear pair; K is the working condition factor of the bevel gear pair; T1 is the torque transmitted by the driving small bevel gear; u is the tooth number ratio of the large and small bevel gears, u = Z2 / Z1.

The bending strength of tooth root is as follows

Where: [σ F] is the allowable bending stress of the tooth root of the bevel gear pair and YFS is the compound tooth form factor.

For the compound tooth shape factor, it can be obtained from Figure 2 according to the equivalent number of teeth.

The boundary conditions of design variables are as follows:

It can be seen from the above mathematical model that the optimal design of the volume and minimum of bevel gear pair can be summarized as a three-dimensional nonlinear constrained optimization problem.