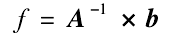A new kurtosis spectral entropy index is proposed, which consists of kurtosis value and envelope spectral entropy. When there are multiple periodic pulses in the rotating machinery, the main components of the envelope spectrum are concentrated in the low frequency band after the envelope spectrum analysis of the periodic signal, which leads to the decrease of the envelope spectrum entropy. Therefore, the envelope spectrum entropy can represent the uniformity of periodic pulse. The more pulses detected, the clearer the envelope spectrum and the smaller the entropy of envelope spectrum. In fact, the proposed kurtosis spectral entropy is the ratio of kurtosis to envelope spectral entropy. This definition not only keeps the original characteristics of MED, but also improves the uniformity of periodic pulse, and considers the effective diagnosis of complex faults.
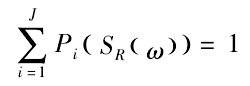
Therefore, the envelope spectrum entropy is defined
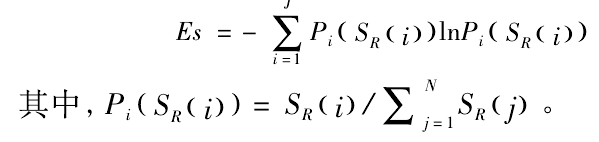
Kurtosis is the impulse characteristic of the signal, and envelope spectral entropy is the periodic characteristic of the signal
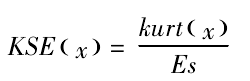
Kurt (x) is the kurtosis of the input signal, and KSE (x) is the kurtosis spectral entropy of the signal. Obviously, for the periodic pulse signal, the envelope spectrum is concentrated in the low frequency region, resulting in the smaller es value. The envelope spectrum entropy of sporadic pulse signal is large, so KSE (x) can reflect the uniformity of periodic pulse signal. EEMD is decomposed to get the same intrinsic mode function, and mksed is used to denoise EEMD to extract more uniform periodic pulse.
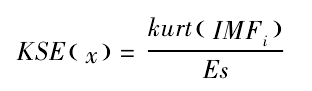
Under the actual working conditions, noise often affects the fault feature extraction. Selecting the appropriate deconvolution index and filter length is the key to extract and analyze the bearing fault features with mk-sed. Using KSE as the objective function of deconvolution can highlight most of the shock signals. Suppose that IMF is a time series X (n)
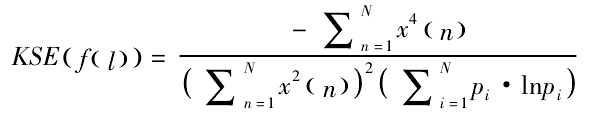
The derivative of the equation with respect to the filter coefficient f is taken and solved to zero
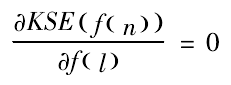
The following equation can be obtained in deconvolution process
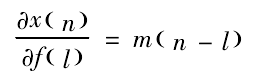
Where m (n) is the output sequence. The formula is introduced into the formula
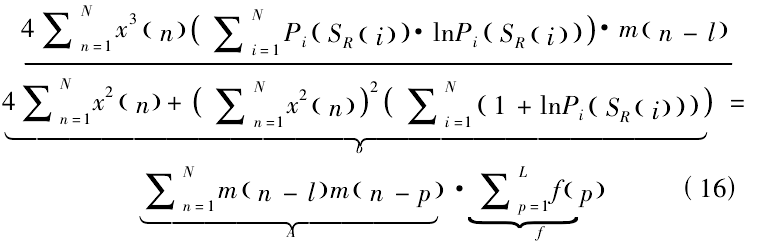
The formula can be expressed in matrix form
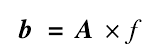
The inverse filter matrix can be obtained by iterative calculation