1. Gear corrugation order noise and analysis
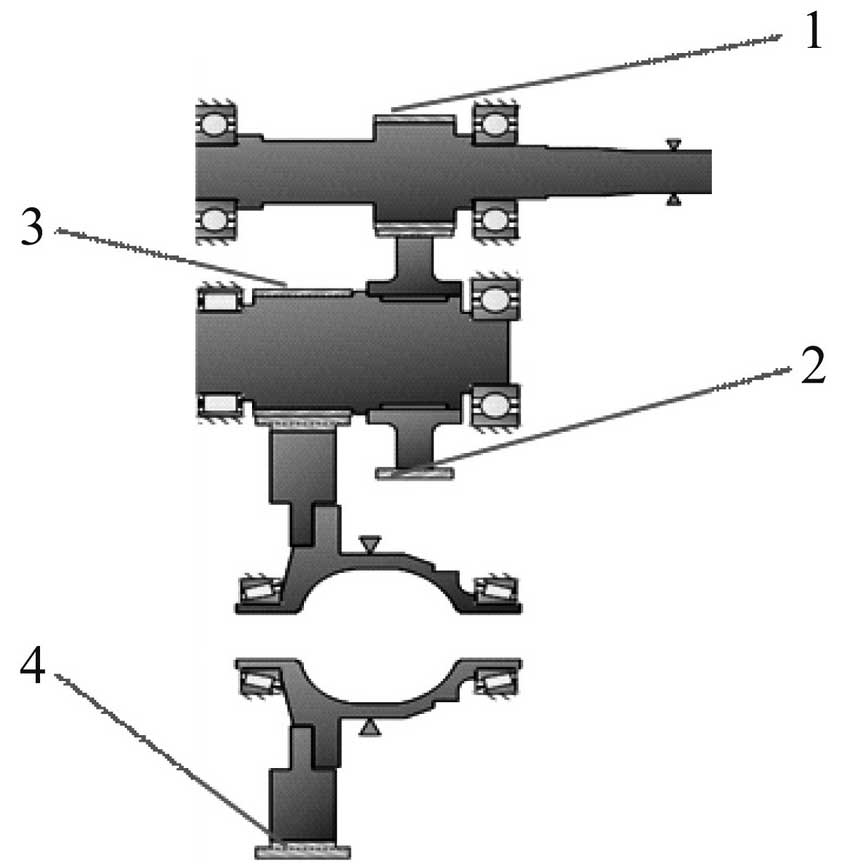
A bewildering “ghost-step” noise occurs in the pre-production stage of a vehicle reducer product development.Fig. 1 is the structural layout of the reducer. The structure of the drive system is relatively simple. There are only two-stage gear drives. Based on the number of teeth of each gear, the basic order of the two pairs of gear pairs can be obtained to four times, as shown in Table 1.All four gears are made by grinding the teeth after quenching heat treatment.It is confirmed by on-site replacement gear checking test that there is abnormal manufacturing and processing on the tooth surface of the driving gear 3 on the intermediate shaft in the figure. The noise of the lower monitoring step is shown as shown in the figure. The abnormal peak order of double 11.7, double 23.5 and triple 35.2 orders of the secondary main and subtracting gear pair foundation occurs.
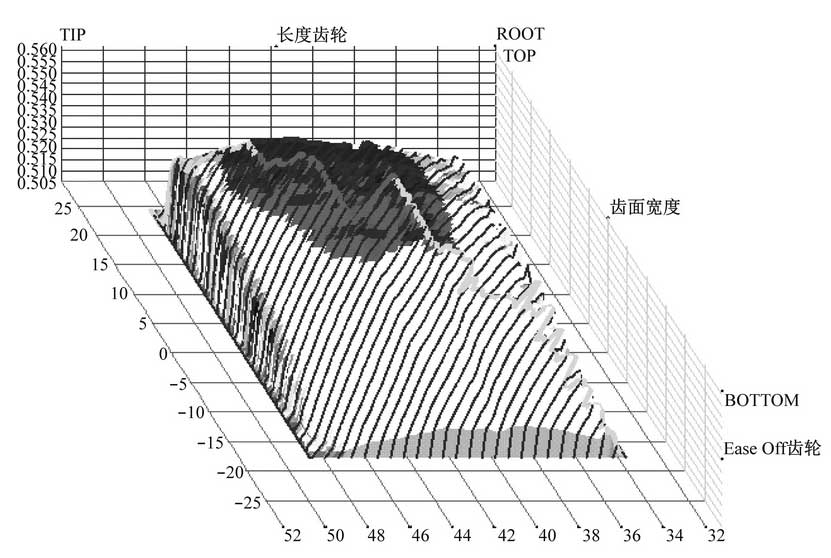
The figure is a three-dimensional topographic View of the gear surface, which can be detected by Taylor-Hopson topograph[2-4]. From the top of the tooth to the root of the tooth and along the diagonal direction of engagement, the waviness curve hidden in the roughness component can be found. Two peaks and one trough are circled in the figure. The arithmetic average height of the peak and trough contour is about 0.02 mm, i.e. 20 um, and the width of one peak or trough is about 10 mm.During the engagement of a tooth surface, a third wave step excitation is formed, i.e. there are doubling, doubling and tripling frequency orders related to the number of teeth in Figure 2.
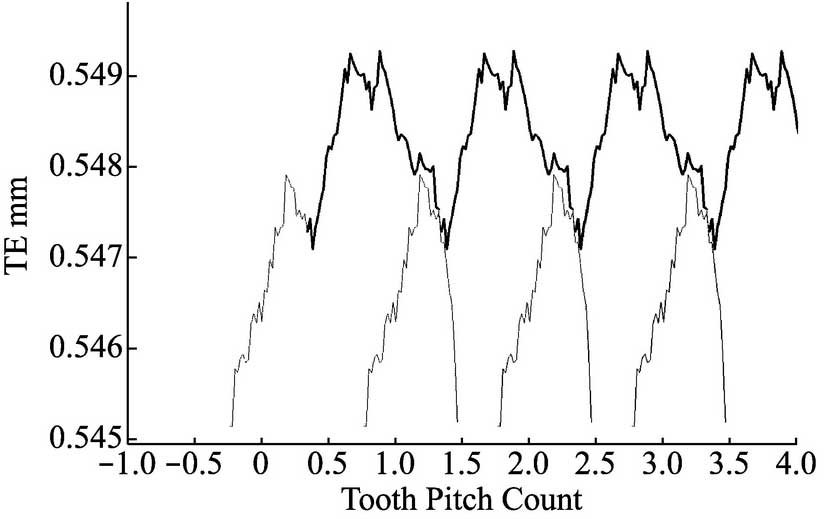
The drawing is a test diagram of the transmission error curve of the gear tooth surface. It can be seen intuitively by using the Grison contact meter that each large waveform represents a tooth pitch and consists of three identical teeth of a gear. Its transmission error value TE is about 0.004 mm.The transfer error curve detection map corresponds to the three-dimensional topographic map, in which the bifurcation waveform circled is also composed of two peaks and one trough.
Based on the above analysis, it can be concluded that there is a strong consistency between the corrugation degree and the transmission error of the tooth surface, i.e. the corrugation error can form a waveform step excitation.In addition, combined with the field analysis and verification results of the problem, it can be seen that only when abnormal dither occurs in gear grinding process and the tooth surface corrugation is more outstanding than other excitation sources of gear pair, will a more prominent frequency multiplication order or obvious gear screeching noise be formed.By improving the grinding process on the grinder, the waviness parameters of the tooth surface can be basically controlled in the range of arithmetic deviation Wa < 13 um of the corrugated profile and the steepness Wku < 4.0 of the corrugated profile.
2. Discussion on gear corrugation order noise mechanism
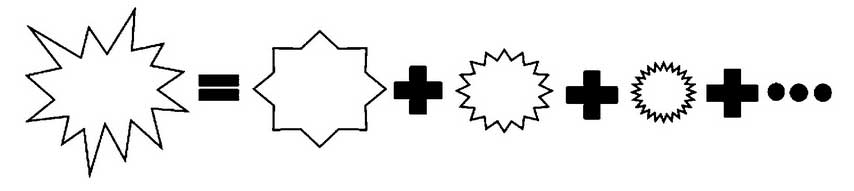
As shown in Fig. 5, for any continuous revolving friction pair, the surface corrugation can constitute an error excitation in geometry of one cycle per revolution, and the geometric error excitation of the continuous revolving can be decomposed into a series of step excitations consisting of waveforms of different sizes.The geometry in the figure can be further described by mathematical methods. As shown in Eq. (1), the geometric error waveform on the left side of the equation can be seen as a continuous integrable waveform on 2kpi over an infinite number of revolving circumferences r, and the decomposition waveform on the right side of the equation can be expanded in time domain t by Fourier series if the rotational speed n is a periodic function R (t):
R(t)=A0+k=1_Aksin(k t+_k)=A0+k=1_akcoskt+bksink t
Where k is an integer, ak=1pi-pi-pi r(t) cosktdt, bk=1pi-pi r(t) sinktdt.From the above formulas, it can be seen that k-integer values correspond to different orders, k=0 represents the global excitation of order 0, and the other positive and negative integers with the same absolute values represent the same order, but the corresponding speed direction is opposite.In the case of inner or outer raceway friction pairs of rolling bearings, k=1 represents the first order of the basic order, k=2, 3, etc. are inferred to the second and third order in turn.In the case of gear-type friction pairs, k=1 is usually the first primary order of the basic order, and is the same as the number of teeth of the active gear Z. The other K values are also analogous in turn, for example, there is a “mid-concave” situation on each tooth surface and the “mid-concave” situation is dominant relative to other excitations; but in the case of many other geometric abnormalities on the tooth surface, such as “S” corrugation on the tooth surface,Then the main order k value formed by this waveform is not necessarily the same as or integer times of the number of teeth Z of the drive gear. For various reasons of machining, the main order k value only does not rotate once with the drive gear, and the number of wave peaks and troughs of similar geometrical magnitude composed of the “S” shape on all teeth is the same. Obviously, since the friction pair of the rotary gear is a function r(t) whose cycle is every revolution of the drive gear,The number of crests and troughs in the form of “S” always has a fixed proportional relationship with the number of teeth of the driving gear and is usually a fractional value proportional relationship, which is commonly referred to as “ghost step” or unknown order in the industry.
It is necessary to add that for actual gear rotating friction pairs, in addition to the geometric waveform excitation of the tooth surface, there are many excitations such as slip excitation due to unsynchronized rolling and sliding speeds, rod-in and rod-out impact caused by elastic deformation of the teeth, and error excitation due to bearing support and assembly.However, this does not affect the geometric error single factor analysis of the surface ripple of friction pair of rotary gear.Therefore, if the order noise of corrugation is to be eliminated, the amplitude of corrugation needs to be reduced below that of other excitation sources, at least not to be the main outstanding excitation.
3. Verification case of gear corrugation order noise improvement

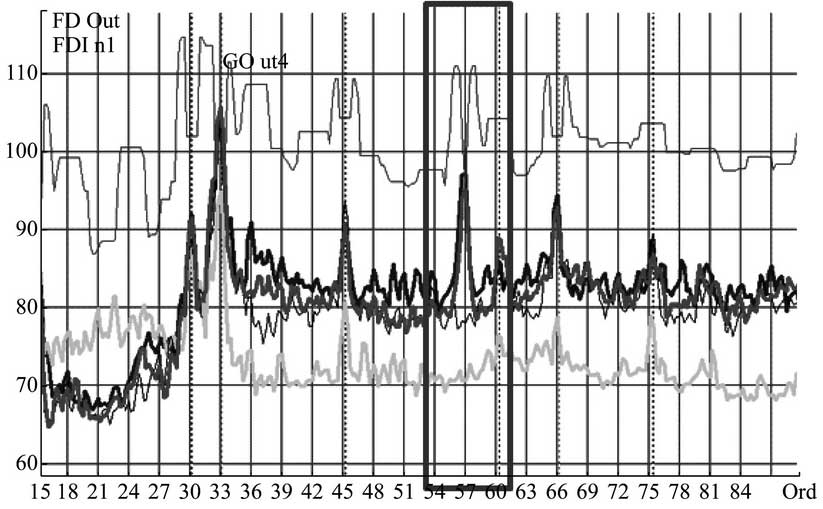
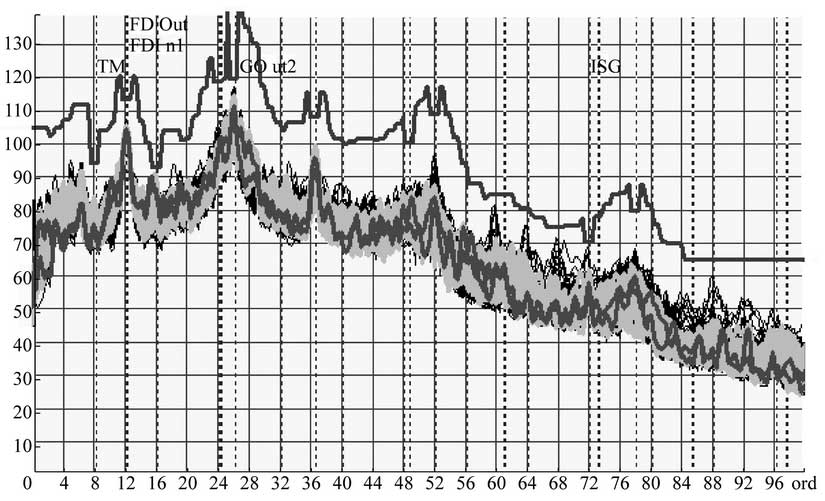
In the PPAP stage of a 6-speed front-drive manual transmission, ghost-step squealing noise occurs in the 4th, 5th and 6th gears. As shown in the table, each ghost-step is not multiplied by the gear-pair order of the gear-shift, but the ratio to the gear-pair order of the main and subtractive gears uniformly points to a fixed percentage value of 3.77, which directly points the spearhead of the problem to the gear-pair of the main and subtractive gears.After replacing the main and driven gears with ABA, the gear is locked further. Then the geometric parameters of the main and driven gears are analyzed after grinding and machining. It is confirmed that the quality of the geometric parameters of the tooth surface and the processing technology problems exist. The actual state of the tooth surface is shown in Figure 6.Figure 7 shows the checking order diagram of the fourth gear on the downline monitoring platform before and after the process improvement of the main reducing gear. If the order is circled by the box, the noise of the “ghost step” of each gear will disappear completely after the improvement.