
1. Introduction
The operating accuracy of spur gear systems is crucial for the performance of transmission systems, especially in complex environments like those in aero engines where tooth surface faults such as wear are common. This has led to extensive research on predicting gear wear and computing meshing stiffness.
1.1 Research Background
Spur gear systems often operate in challenging conditions, leading to tooth surface faults. Tooth surface wear is an inevitable fault during actual operation, significantly affecting the meshing performance and dynamic characteristics of the transmission system.
1.2 Previous Research
- Wear Depth Prediction and Meshing Stiffness Computation: Many studies have relied on Archard’s wear theory. For example, SHEN et al analyzed the impact of wear on planetary gear meshing characteristics and calculated related parameters. Others, like HUANGFU et al, proposed 3D wear prediction models considering various factors.
- Friction and Contact Models: Research has also focused on friction during tooth contact. DROZDOV et al developed a fractal contact stiffness model, and BENEDICT et al studied empirical formulas for friction coefficient prediction.
1.3 Limitations of Current Research
- Most research combines fractal contact theory with analytical methods mainly for solving TVMS of spur gear pairs without faults, and computational accuracy needs improvement.
- Many studies on surface wear faults are based on 2D fractal methods or focus on wear depth prediction, lacking in-depth analysis of the real contact form’s influence on wear faults.
2. TVMS Model of Spur Gear Pair with Tooth Surface Wear Fault Based on Improved LTCA Method
2.1 TVMS Model of Spur Gear Pair by LTCA Method
The meshing process of spur gear pair can be seen as the contact of two elastomers. The deformation coordination condition at the instantaneous contact point is given by
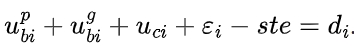
Bending shear deformation has a linear relationship with spur gear tooth load, and expressions for and are provided. The contact compliance matrix is also defined. By transforming the equations, an iterative solution method for contact forces is obtained, and the meshing stiffness of spur gear pair can be calculated as .
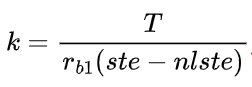
2.2 Friction Coefficient Introduced into the TVMS Model
In actual gear meshing, there is a combination of rolling and sliding, and relative sliding speed exists. Variation of time-varying friction on both sides of the pitch circle affects gear meshing stiffness. Considering the slippage due to friction, a new deformation coordination condition for spur gear system is derived as .
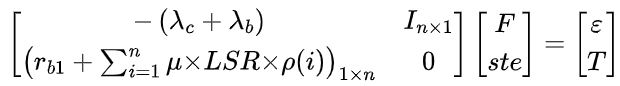
2.3 Considering the Effect of Normal Microconvex Body Fractal
The actual tooth surface is not smooth, and the fractal theory’s W-M function is suitable for describing it. For 3D fractal analysis, the micro-convex body on a rough surface is equivalent to an elastic halfspace body. Various equations for contact radius, cross-sectional area, peak deformation, and contact stiffness of the micro-convex body are derived. The global stiffness considering normal fractal contact stiffness is obtained through integration.
2.4 Improved TVMS Model in Tooth Surface Wear Fault Condition
Assuming identical teeth after wear, the spur gear surface wear fault changes the spur gear profile deviation and load distribution coefficient. To balance efficiency and accuracy, the tooth profile is updated when the wear depth reaches a certain threshold. The LTCA method is used to calculate meshing stiffness and load distribution coefficients, and the wear depth is calculated according to Archard’s wear theory. The wear cycle is iteratively solved until the accumulated wear depth reaches the predefined maximum.
3. Model Comparison and Validation
3.1 Model Establishment
Considering the actual tooth surface morphology and contact form, combined with friction force and 3D fractal contact theory, an improved TVMS model of spur gear pair with tooth surface wear fault is established. The main dimension parameters of the spur gear pair are shown in Table 1.
| Nomenclature | Number of gear teeth | Normal module/ mm | Tooth width/ mm | Pressure angle/(o) | Radius of inner hole/ mm | Tooth top height factor | Top gap coefficient | Elastic modulus/ GPa | Poisson ratio | Gear torque/ (N·m) |
|---|---|---|---|---|---|---|---|---|---|---|
| Pinion/gear | 20/40 | 1 | 10 | 20 | 4/5 | 1 | 0.25 | 212 | 0.3 | 20 |
3.2 Comparison Results
The TVMS results obtained by considering 3D fractal theory and friction are compared with those from other methods. they are numerically closer to a reference result compared to Hertz contact theory. The direction change of the friction force between gear teeth at the pitch circle position causes a small mutation in TVMS, demonstrating the accuracy of the proposed method.
4. Analysis of the Meshing Characteristics of Spur Gear Pair with Tooth Surface Wear Fault
4.1 Predictive Analysis of Wear Models Considering Tooth Roughness
- Wear Depth Analysis: The wear depth is mainly affected by relative slip speed and contact pressure. Severe wear occurs at the root of pinion teeth. The wear depths calculated by different methods show that the empirical formula gives a more continuous result, while the proposed method has some fluctuations. The wear depth increases rapidly in the early wear period and then slows down.
- TVMS Variation: The TVMS decreases more in the initial wear cycle, corresponding to the wear depth change. As the wear cycle progresses, the tooth surfaces become smoother, and the TVMS has a minor abrupt change at the pitch line due to friction. The variation of tooth surface wear depth with and without considering fractal effects is compared, showing differences in wear distribution.
4.2 Effect of Friction Coefficient on Tooth Wear Fault
Setting specific fractal parameters, the TVMS of spur gear pair under different friction coefficients and wear cycles is calculated. As the friction coefficient increases, the TVMS in the meshing region of two pairs of spur gear teeth decreases, and there is an abrupt change in meshing stiffness within the pitch line region. The wear depth at the non-pitch line increases with the increase of wear cycles and friction coefficient.
4.3 Effect of Tooth Roughness on Tooth Wear Fault
With a fixed friction coefficient, the changes in wear depth under different surface roughness levels are analyzed. As the fractal dimension increases, the TVMS in the meshing region of both pairs of spur gear teeth increases. The wear depth on the tooth surface at the non-pitch line increases with wear cycles but decreases with an increasing fractal dimension. In the case of lower wear cycle, the influence of friction coefficient on TVMS and wear depth is more sensitive, but as the wear cycle increases, the influence of fractal dimension becomes more pronounced.
5. Conclusions
- TVMS Comparison: Compared with the TVMS solved by Hertz contact theory, considering friction causes a mutation at the pitch line position, and considering 3D fractal theory increases it to a certain extent.
- Wear Depth and Fault Progression: Considering 3D fractal contact and friction, wear depth is uneven in the early stage of tooth surface wear fault with small spalling as the main form. As wear cycles increase, spur gear wear depth stabilizes, and minor spalling faults are replaced by general wear fault.
- Influence of Friction and Fractal Dimension: With an increase in friction coefficient, the mutation of TVMS at the pitch line is more obvious. Under tooth surface wear fault, an increase in friction coefficient and a reduction in fractal dimension decrease the TMVS in the meshing cycle of two pairs of spur gear teeth and increase the wear depth at non-nodal positions. As wear cycles increase, the influence of fractal dimension on TVMS and wear depth exceeds that of the friction coefficient.
In summary, this study provides a comprehensive analysis of the meshing characteristics of spur gear pairs with tooth surface wear faults, considering various factors and improving the understanding of gear behavior under such conditions.
