At present, there are mainly analytical method, numerical method and experimental method to solve the dynamic analysis model of mechanical system. Because most of the dynamic equations are complex, it is difficult to get the analytical solutions of the equations, so the numerical method is usually used to solve the dynamic equations. The nonlinear differential equations set up in the part of planetary gear transmission system can not get accurate analytical solutions because of the strong nonlinear factors of backlash and time-varying meshing stiffness. Therefore, this paper also uses the numerical method to solve the equations.
Runge Kutta method is widely used in solving dynamic differential equations because of its high accuracy. With the development of science and technology, the wide application of computer and the rapid development of Applied Mathematics, Runge Kutta method with strong generality and high precision has been further popularized.
The dynamic differential equations of the system are usually a nonlinear system of second-order multivariate differential equations
For the system of second order differential equations with multiple variables:
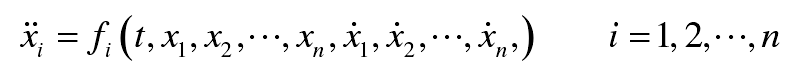
Through transformation, the second order differential equations of the formula can be rewritten into the first order differential equations as follows:
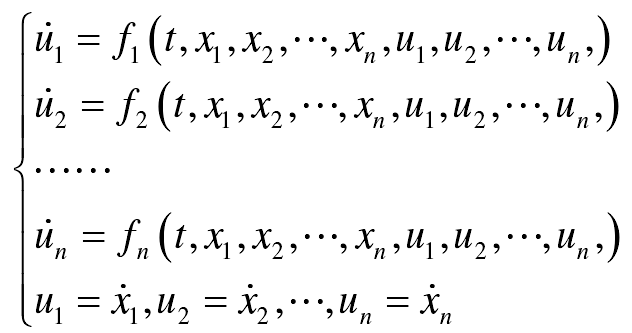
Let the step length of integration be H. when the corresponding values of Xi and j at TJ are known, then Xi, j + 1 can be obtained from TJ to TJ + 1
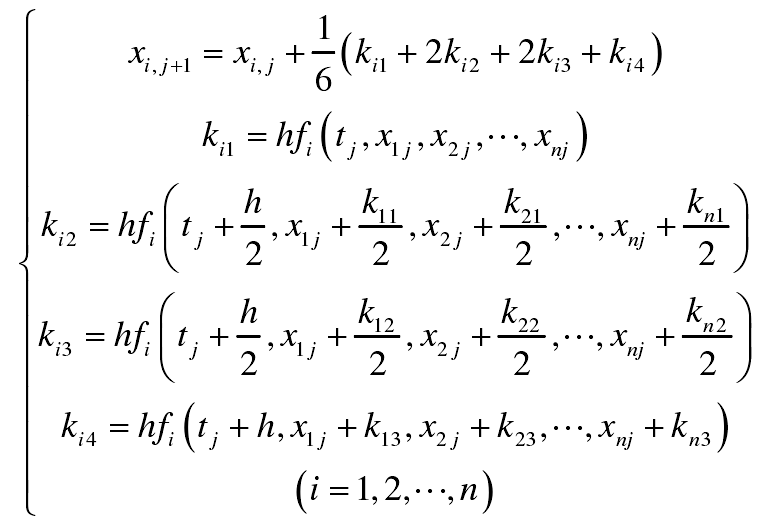
The formula is the basic Runge Kutta formula with fixed step size. However, in order to improve the convergence stability and calculation accuracy, variable step size is used in this paper.
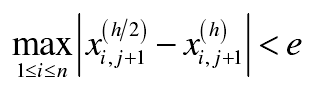
Then we can continue to solve Xi, j + 2; if the condition is not satisfied, the step length will be halved and calculated until the condition is satisfied. Where:
E — calculation accuracy.
