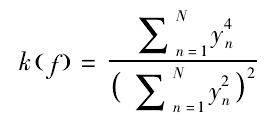Med is to eliminate the influence of transmission path by optimizing the filter. xn(n = 1,2,… , n) is the input vibration signal sequence, including random noise, periodic shock, harmonic, etc. It consists of input signal xn and FIR filter f = F1, F2 [,…] The output signal generated by [F] l can be expressed as follows:
The output yn should be consistent with the pulse signal of the original signal as far as possible. If the impulse signal corresponds to a larger kurtosis value, the Med filter must maximize the kurtosis of the output signal. The kurtosis of the zero mean value of the output signal yn is defined as follows:
The optimal solution of output signal kurtosis maximization is foptimal, K (f) optimal ≥ K (f), f ∈ RL, RL is an L-dimensional Euclidean space, K is the kurtosis in the formula, f is a filter of any length L.
Med is based on kurtosis maximization instead of entropy minimization. Although there is a certain relationship between kurtosis and entropy, its basis is still kurtosis maximization. Therefore, Med finds the source with the maximum kurtosis, not the minimum entropy. This is the most important reason for the simplification of MED results.