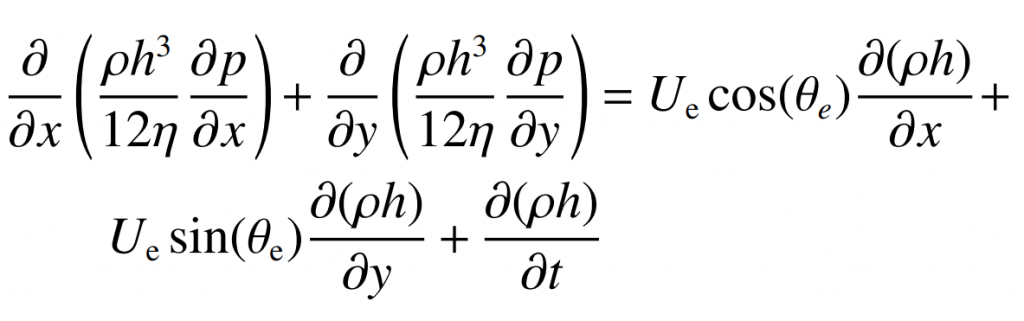The point contact problem of conjugate surface of spiral bevel gear can be represented by the elliptical contact model shown in the figure In the figure, UA and UB are the unit vectors of the long and short semi axes of the contact ellipse, θ E and θ S is the angle between the entrainment velocity vector and the relative sliding velocity vector and the short half axis of the ellipse, that is, the angle with the X axis, which can be calculated by the following formula:
The pressure distribution in the elliptical contact area of spiral bevel gear is obtained by solving the Reynolds equation. The Reynolds equation considering the included angle of entrainment is:
Where: H is the thickness of lubricating oil film, P is the contact pressure, ρ Is the lubricating oil density, η Is the viscosity of lubricating oil.
The oil film thickness h at any contact position is:
Where: H0 (T) is the initial central film thickness, RX and ry are the radius of curvature along the minor axis and major axis of the contact ellipse, δ 1 , δ 2 is the true roughness of two contact surfaces, and V (x, y, t) is the local contact deformation, which is calculated by Boussinesq integral:
Viscosity is a function of pressure, expressed by the following formula:
Density can also be expressed as a function of pressure:
The load balance equation is:
In the case of actual contact, the friction characteristics are coupled with the temperature rise The viscoelastic non-Newtonian fluid is used to solve the shear of lubricating fluid:
Where: ultimate shear stress τ 50. The ultimate shear modulus G ∞ is a function of pressure and temperature, and its calculation method is as follows:
The friction solution includes two parts: lubrication fluid shear and roughness contact. The friction at the conjugate contact point of spiral bevel gear can be obtained by integrating the shear stress in the whole contact area. The temperature effect coupled with the friction coefficient is calculated by the following formula:
The friction coefficient is solved as: