Modal analysis of driven gear in Abaqus, material properties of spiral bevel gear: elastic modulus E=207 GPa, Poisson’s ratio μ = 0.25, density ρ = 7. 86 × 103kg /m3。 The large wheel model is meshed, and the mesh type is finally determined as quadric tetrahedral element with 549466 elements and a mesh size of 3 mm, taking into account the calculation accuracy and calculation scale, as shown in Figure 1.
The boundary condition is set as follows: fix the central shaft hole of the spiral bevel gear, simulate the constraint of the bearing on the shaft with the elastic element, and give it rigidity. The Lanczos method is used for modal analysis of spiral bevel gears with circular hole structure. The sum of the effective modal masses of the translational mode should be approximately equal to the structural mass. The mass of the big wheel is 9 86 kg, after several trial calculations, calculate the mode within the frequency range of 10 500 Hz, and the effective modal masses in X, Y and Z directions are respectively 99% of the structure mass 82%、99. 32%、99. 90%, meeting the requirements of modal analysis, ensuring the accuracy of the subsequent modal superposition method to calculate the dynamic response.
The resonance of spiral bevel gear system shall meet the following conditions: the frequency of excitation force is equal to the natural frequency of the system; The harmonic order of excitation force K is equal to the pitch diameter of spiral bevel gear m. Because the meshing force is mainly the first harmonic, the modes at a pitch diameter are analyzed in detail. Extract the first six natural frequencies and calculate the frequency margin between them and the main frequency of the meshing force, as shown in the table. Where, the frequency margin M is:
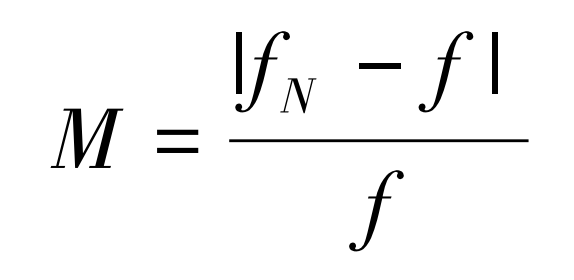
Where, fN is the N-th natural frequency of the big wheel; F is the dominant frequency of the excitation force, and the corresponding f value in this paper is 9 405 Hz.
| Order | Natural frequency /Hz | Frequency margin /% |
| 1 | 291.2 | 96.90 |
| 2 | 1 056.6 | 88.77 |
| 3 | 1 137.8 | 87.90 |
| 4 | 1 426.0 | 84.84 |
| 5 | 1 426.0 | 84.84 |
| 6 | 1 708.5 | 81.83 |
In order to reduce the occurrence of resonance, the frequency margin should be more than 15%. According to the table, the frequency margin between the first six natural frequencies and the main frequency of the excitation force is more than 80%, so the large wheel will not resonate.

The first six modal vibration modes of the circular hole gear structure are as shown in Figure 2. The first and sixth modal vibration modes are pitch circle vibration, with the same displacement at the periphery; The second and third vibration modes are one-pitch radial vibration, and the fourth and fifth vibration modes are two-pitch radial vibration. The analysis shows that the vibration mode of the large wheel is regular, and its vibration form conforms to the disk structure.
