| Parameter | Hypoid gear wheel | Hypoid gear pinion |
| Number of teeth | 6 | 38 |
| Outer end diameter /mm | 100.24 | 380.6 |
| Average pressure angle / ° | 22.5 | 22.5 |
| Offset distance of small wheel /mm | 38 | 38 |
| Intersection angle of gear countershaft / ° | 90 | 90 |
| Tooth surface width /mm | 48 | 48 |
| Helix angle / ° | 50 | 37.09 |
| Pitch cone angle / ° | 10.92 | 78.81 |
| Face cone angle / ° | 14.83 | 79.30 |
| Root cone angle / ° | 10.43 | 74.80 |
| Rotation direction | left rotation | right rotation |
| Distance from face cone vertex to intersection /mm | 3.3128 | 0.2183 |
| Distance from root cone vertex to intersection /mm | -3.0491 | -0.0064 |
| Distance from outer wheel crown to intersection /mm | 185.99 | 35.78 |
Matlab is used to calculate the tooth surface points and solve the tooth surface equations, and solidworks2012 is used to establish the blank model of the hypoid gear. Now the parameters required for the three-dimensional modeling of the studied hypoid gear pair are listed in Table 1 and table 2 below.
| Parameter | Convex surface of hypoid gear pinion | Concave surface of hypoid gear wheel |
| Tip radius /mm | 158.195 | 154.56 |
| Tooth profile angle / ° | -27 | -22.5 |
| Radial tool position /mm | 147.7926 | 141.8567 |
| Angular tool position / ° | 69.12 | 57.12 |
| Wheel blank installation angle / ° | 10.43 | 74.80 |
| Vertical wheel position /mm | 38.1528 | -2.3472 |
| Bed /mm | -1.2094 | 1.2689 |
| Axial wheel position correction value /mm | 3.6316 | -1.9152 |
| Roll ratio | 6.4074 | 1.0027 |
1.Large wheel blank model
According to the parameters shown in Table 1 and table 2, use matlab to solve the equation group of hypoid gear large tooth surface, and 45 groups of tooth surface point parameter values can be obtained, which can be substituted into the equation of hypoid gear large tooth surface. Then, through coordinate system transformation, the coordinate values of the tooth surface points of hypoid gear large wheel in the wheel blank coordinate system can be obtained. Input the coordinate points into SolidWorks, and use the curve fitting tool provided in the background of SolidWorks, The tooth surface model of hypoid gear can be generated, and finally the modeling of large gear can be completed. The established model of large wheel blank of hypoid gear is shown in Figure 1 below.

2.Small wheel blank model
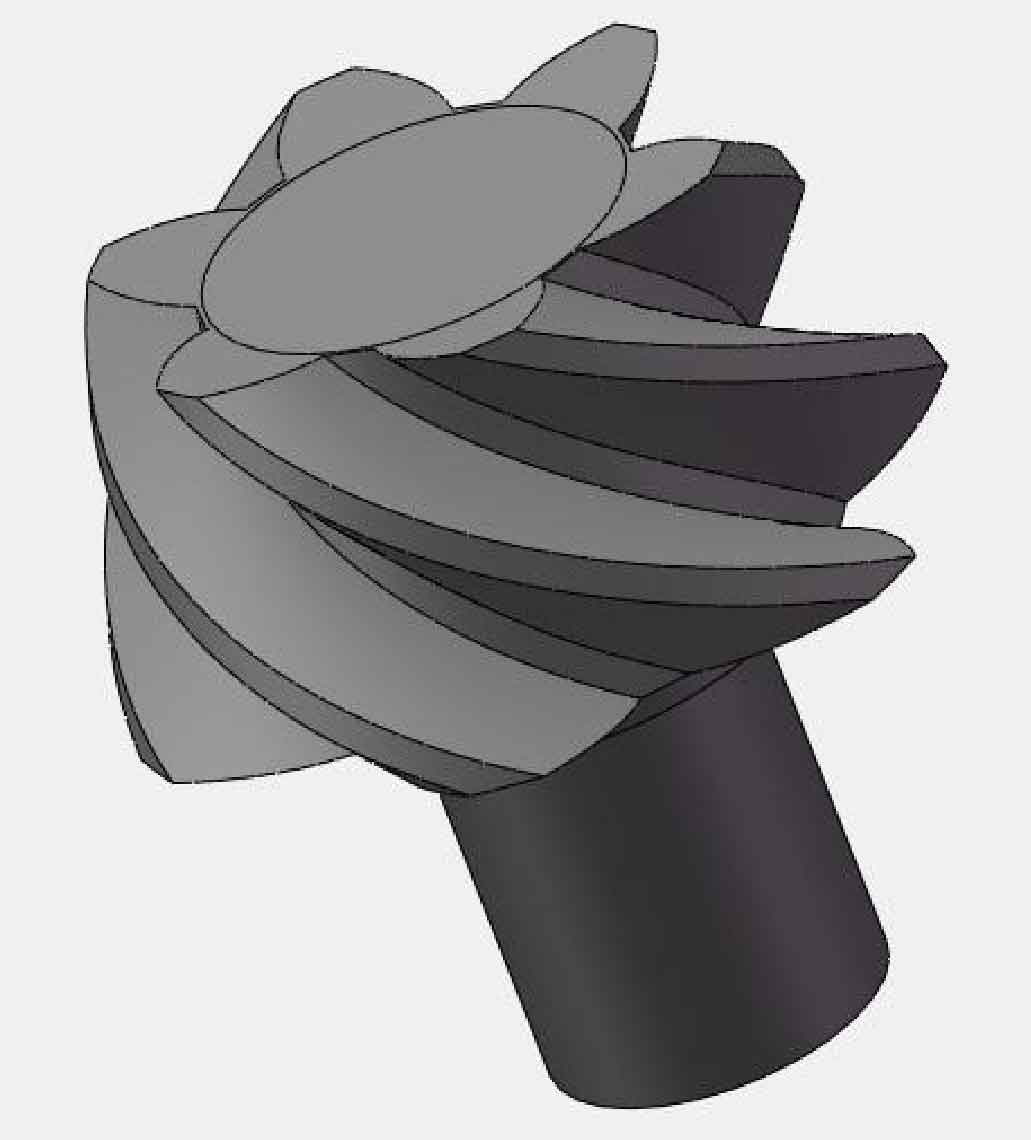
According to the parameters shown in Table 1 and table 2, 45 sets of tooth point parameter values can be obtained by using MATLAB to solve the tooth surface equation group of hypoid gear pinion, which can be substituted into the tooth surface equation of hypoid gear pinion, and then the tooth point coordinate values of the pinion in the wheel blank coordinate system can be obtained through coordinate system transformation. The difference between the tooth point calculation process of hypoid gear pinion and the general theory is that the influence of deformation mechanism needs to be considered, The actual roll ratio is variable. Input the coordinate points into SolidWorks, and use the curve fitting tool provided in the background of SolidWorks to generate the tooth surface model, and finally complete the modeling of small wheel blank. The established hypoid gear small wheel blank model is shown in Figure 2 below.