In the previous discussion, we can know that the spatial conjugate curve is actually the contact line of the tooth surface during meshing. The third and fourth chapters study the case of single pair of spatial conjugate curves, that is, there is only one contact line on each tooth surface and only one contact point at each instant. However, as an assumption, if multiple spatial curves are selected on a tooth surface and their spatial conjugate curves are obtained, and the corresponding tooth surface is constructed according to these spatial conjugate curves, there are multiple contact lines on each tooth surface, that is, there are multiple contact points at each instant. When the instantaneous contact point is expanded from one to multiple, the load between tooth surfaces will be shared by multiple contact points, which may reduce the load on a single instantaneous contact point and reduce the contact stress. Therefore, this paper mainly studies the properties of multi-point contact conjugate curve bevel gear, that is, the bevel gear with multiple spatial conjugate curves on the tooth surface.
According to the previous discussion, the spatial curve and its corresponding conjugate curve are actually the contact lines corresponding to the two bevel gears. If multiple spatial curves are taken in the driving gear coordinate system and their corresponding multiple spatial conjugate curves are obtained in the driven gear coordinate system, and then the tooth surfaces of the two bevel gears are constructed according to these curves, there are multiple contact traces in the meshing of the two bevel gears, That is, at each instant, there are multiple contact points between the two tooth surfaces, so as to realize multi-point contact. Since the multi-point contact has more contact points than the single point contact, the load is shared, which helps to reduce the contact stress of the tooth surface. According to the conjugate curve principle, there are two construction methods for the tooth surface of multi-point contact bevel gear:
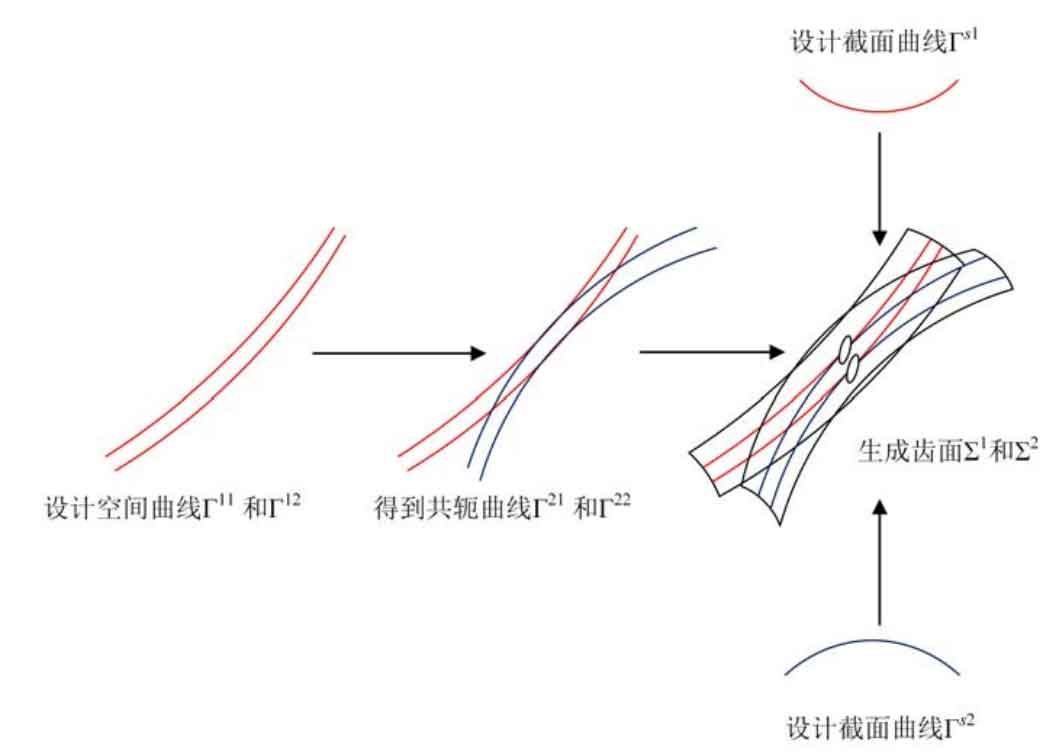
1) Firstly, select multiple spatial curves and obtain their spatial conjugate curves, and then construct the tooth surfaces of driving wheel and driven wheel respectively according to these spatial curves and their spatial conjugate curves (as shown in Figure 1);
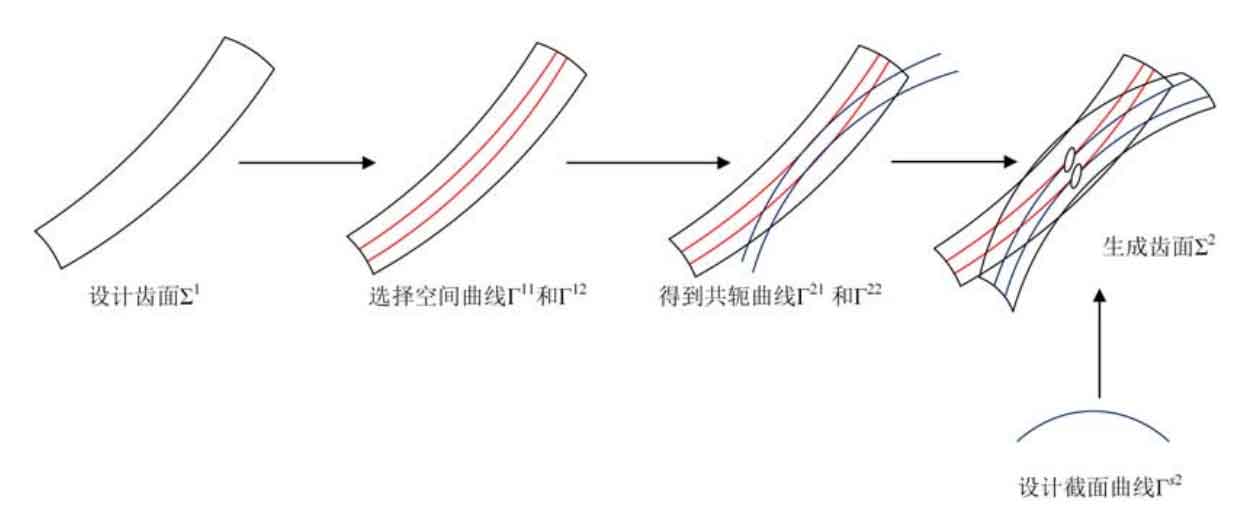
2) First construct the driving gear tooth surface, then select multiple contact lines on the driving gear tooth surface and obtain its spatial conjugate curve, and finally construct the driven gear tooth surface according to the spatial conjugate curve (as shown in Figure 2)