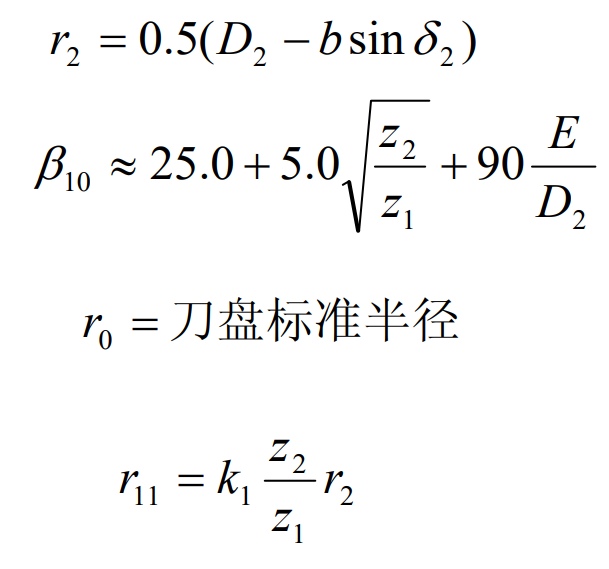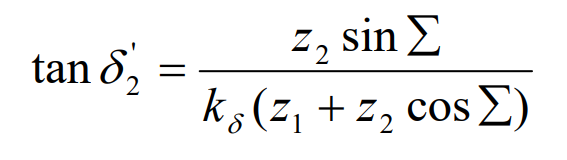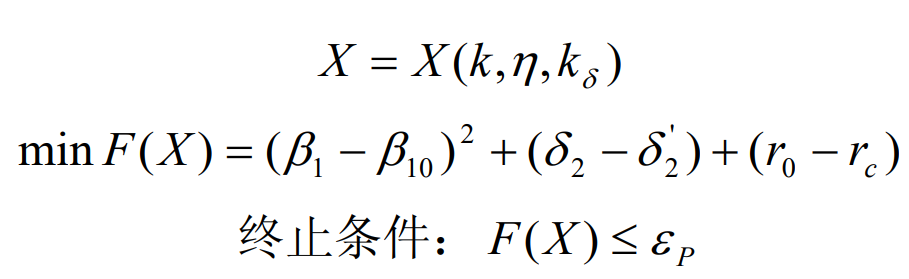According to the Gleason algorithm, the mathematical model of hypoid gear always has 16 independent equations, and its central axis intersection angle Ε , The pinion offset e is the basic parameter of the initially given gear pair, which depends on the structural form of the whole transmission system, α It is the standard value determined by the tooth profile shape, and other parameters ε’、ε 、η 、 δ 2 、 δ 1、 r2 、 r1 、R1、R2、Z 、ZP 、G 、 ZG 、 β 2、 β 1、 α 、 α* 、 k. R0 and R * are 20 parameters in total. Obviously, the values of each parameter cannot be obtained. By expressing the four constraints given by Gleason with specific parameter relations, the following four expressions can be obtained:
The above four equations, together with the sixteen equations of the previous mathematical model, constitute the geometric parameter equations of hypoid gear. There are 20 equations in total, which are used to solve 20 unknown variables. Obviously, the definite solution can be obtained.
Summarize the geometric parameter calculation method of hypoid gear formulated by Gleason company. The core idea is to determine a fixed calculation process first, and solve it with the specified equation in each step of the calculation process. According to the four conditions set by Gleason company, the Gleason geometric parameter design method with manual calculation as the calculation condition has three defects, that is, the calculated big gear node is often offset from the midpoint of tooth width, the calculation error of pinion helix angle is large, and there is an error between the calculated cutterhead radius and the standard tool parameters, resulting in the inability to select the tool clearly.
The solution idea of Gleason algorithm is based on manual calculation, so the calculation relationship is required to be as simple as possible to ensure the calculation efficiency and accuracy. Based on the solution idea of Gleason’s geometric parameters, this paper proposes to increase the 16 equations to 20 equations in the mathematical model of Gleason’s geometric parameters design, and solve 20 parameters with the simultaneous equations of 20 independent equations. In order to ensure that the node P is located at the midpoint of the tooth width in the meshing process of hypoid gear pair, the adjustment coefficient K of large gear pitch cone angle is increased δ , That is, during the initial calculation of the node radius of the big gear, the pitch cone angle of the big gear is determined by the following formula:
In the initial calculation of the pitch circle radius of the big gear, set the adjustment coefficient of the pitch cone angle of the big gear as K δ= 1.2 at the same time, the constraint condition is put forward, that is, the initial value of the pitch cone angle of the large gear is equal to the actual value.
Starting from the geometric design idea of Gleason made hypoid gear and combined with the idea of optimization design theory, this paper explores a new design method to ensure that more accurate parameters are obtained than Gleason algorithm. The new design method is based on the least square method in the optimization design theory, and the parameter step-by-step approximation solution method is used to replace the formula for direct solution. The specific mathematical model is as follows:
According to the optimization design theory, the above calculation model is a nonlinear least squares mathematical model, which can be solved by guess Newton method.