In marine engineering, the stability of vessels during anchoring operations is critical, especially when external forces like wind, waves, and currents exert substantial loads on the anchor chain. Traditional anchoring systems, such as electric or hydraulic windlasses, often fail to provide reliable self-locking under high-stress conditions, leading to unintended chain release and potential accidents like grounding or collisions. To address this, I have developed a novel self-locking device based on worm gear principles, which enhances safety by integrating advanced control systems and dual-worm configurations. This design not only improves the self-locking capability but also optimizes power transmission and lubrication management. In this article, I will detail the theoretical foundations, design requirements, component selection, and performance analysis of this innovative worm gear system, supported by mathematical models and comparative tables to illustrate key parameters.
The core of this innovation lies in leveraging the inherent self-locking properties of worm gear mechanisms, where the worm’s lead angle is designed to be smaller than the friction angle, preventing back-driving under load. Traditional worm gear systems, however, suffer from inefficiencies due to high friction losses and sensitivity to lubrication, which can compromise self-locking. My approach incorporates a dual-worm setup coupled with a Programmable Logic Controller (PLC) for real-time monitoring and control, ensuring precise chain length management and adaptive response to dynamic conditions. Below, I will explore the fundamental principles, identify limitations of existing systems, and present my design methodology, including calculations for torque, material selection, and motor sizing, all aimed at achieving a robust solution for marine applications.
Worm gear systems are widely used in heavy machinery for their high reduction ratios and self-locking potential. The self-locking condition for a worm gear is defined by the relationship between the lead angle (φ) and the friction angle (ρ). Specifically, self-locking occurs when φ < ρ, which can be derived from the equilibrium of forces on an inclined plane. For a worm gear, the tangential force required to drive the system must overcome the frictional resistance, and this is expressed mathematically as:
$$ \phi < \tan^{-1}(\mu) $$
where μ is the coefficient of friction. In practical terms, this means that for a given material pair, such as steel and bronze, the lead angle must be kept below a threshold to ensure self-locking. For instance, with a friction coefficient of 0.6, the lead angle should be less than approximately 3.5° to maintain reliable self-locking. However, variations in lubrication and operational wear can alter μ, leading to unpredictable behavior. To quantify this, I have compiled a table of typical friction angles and their corresponding lead angles for common worm gear materials:
| Material Pair | Friction Coefficient (μ) | Maximum Lead Angle for Self-locking (°) |
|---|---|---|
| Steel vs. Bronze | 0.6 | 3.5 |
| Steel vs. Cast Iron | 0.7 | 4.1 |
| Hardened Steel vs. Polymer | 0.8 | 4.6 |
This table highlights the sensitivity of self-locking to material properties, underscoring the need for careful selection in marine environments where corrosion and fatigue are concerns. Additionally, the efficiency of a worm gear transmission is generally low due to sliding friction, which I account for in my design by optimizing the gear geometry and incorporating lubrication control.
One major issue with conventional worm gear self-locking is the degradation under vibration and variable lubrication. In marine settings, ship motions can induce dynamic loads that transition static friction to kinetic friction, increasing μ and potentially violating the self-locking condition. Moreover, lubrication layers can reduce effective friction, leading to inadvertent slippage. To model this, I consider the force equilibrium where the output torque T2 must satisfy:
$$ T_2 = T_1 \cdot \eta \cdot i $$
where T1 is the input torque, η is the efficiency, and i is the gear ratio. For self-locking, the reverse efficiency should be negligible, which is achieved when the lead angle is sufficiently small. However, practical tests show that even minor increases in φ due to wear can disable self-locking. Therefore, my design includes redundant locking through dual worms and real-time adjustment via PLC, ensuring stability across operational scenarios.
The design requirements for this novel marine worm gear self-locking device were established based on industry standards such as GB/T 549-2017 for anchor chains, which specify maximum loads up to 476 kN. Key objectives include achieving a compact form factor, high reliability, and adaptive control. Specifically, the worm gear must have a module near 15 mm to handle high torques, and the system should incorporate automated lubrication to minimize maintenance. The motor power is constrained between 30 kW and 50 kW to balance performance and energy efficiency. To meet these, I focused on the following aspects: dual-worm configuration for enhanced self-locking, PLC-based sensors for monitoring chain length and load, and a synchronization mechanism for gear ratio adjustment.
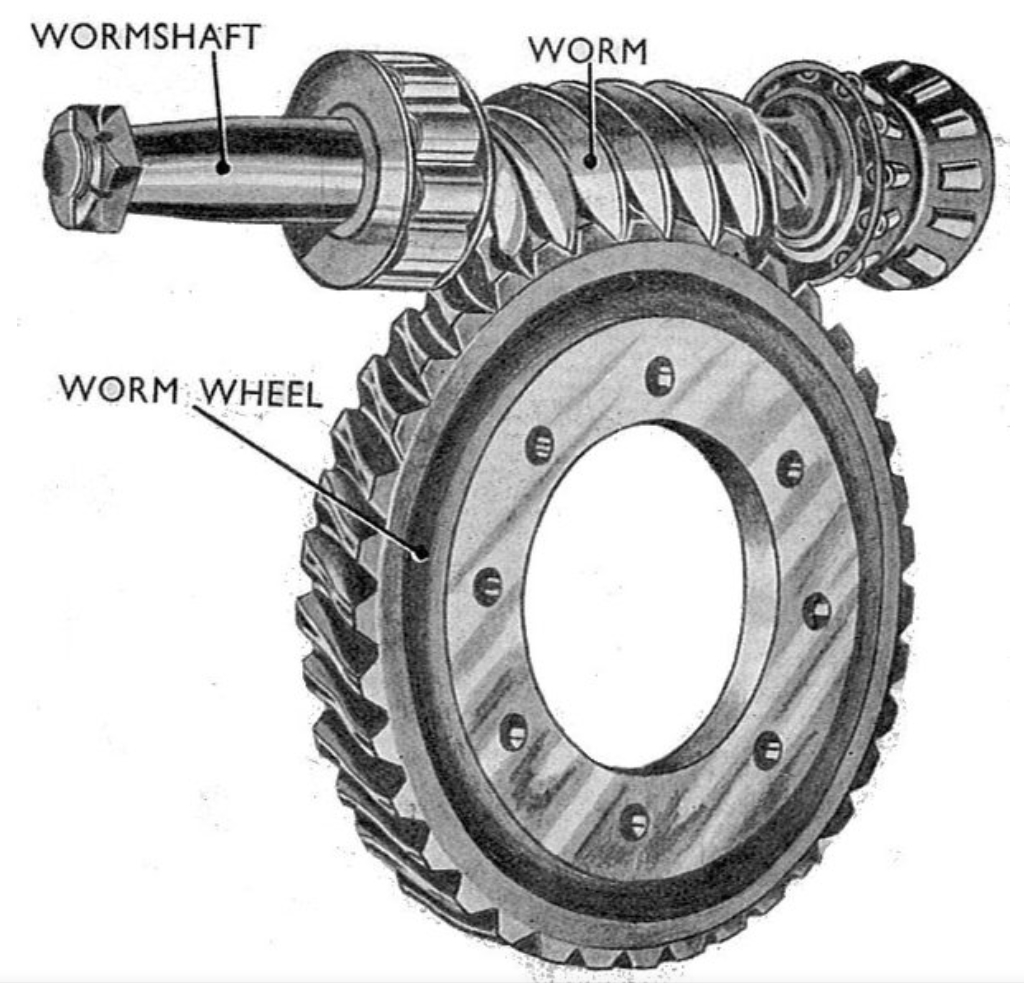
The working principle of my worm gear self-locking device involves three main subsystems: the transmission assembly, lubrication system, and control unit. During operation, the worm acts as the driver when retracting the anchor chain, providing high reduction ratios for efficient pulling. Conversely, when external forces attempt to reverse the motion, the worm gear becomes the driver, and the self-locking mechanism engages to prevent uncontrolled release. The PLC continuously monitors parameters such as chain position, speed, and oil levels through sensors, adjusting the electromagnetic clutch and synchronizer to switch between single-stage and multi-stage inputs. This dynamic control allows for optimal torque management and rapid response to changing conditions.
For instance, in the retraction phase, the PLC processes signals from position and speed sensors to determine the required gear ratio. If the anchor is nearing its stowed position, the system reduces the ratio to minimize inertial effects before engaging the lock. The lubrication system, featuring an activated carbon罐 for oil vapor recovery and precise nozzle injection, ensures consistent friction characteristics. The self-locking force is calculated based on the chain load, which I derived from standard anchor data. For a typical AM3-24 chain with a mass of 12.61 kg/m and a length of 165 m (6 sections of 27.5 m), the total force includes both tensile and gravitational components. The torque on the worm gear connection shaft is given by:
$$ T_1 = F \cdot r $$
where F is the resultant force and r is the effective radius. Assuming a force of 332 kN and accounting for dynamic factors, T1 is approximately 55,110 N·mm. This torque is used as the basis for selecting the worm gear components and motor.
In the selection and design of the worm gear, I prioritized materials and dimensions that ensure durability and self-locking. The worm is made from 20Cr steel, surface-hardened to 58-63 HRC, while the worm gear uses ZCuSn5Pb5Zn5 bronze for its excellent wear resistance and low friction. The design parameters include module m, number of teeth z, and center distance a. For a target gear ratio of 50, I chose a single-start worm (z1 = 1) and a worm gear with z2 = 50. The center distance is calculated to withstand the operational loads, with an initial estimate derived from:
$$ a \geq \left( K_A \cdot T_2 \cdot \frac{Z_E \cdot Z_\rho}{\sigma_H} \right)^{1/3} $$
where KA is the application factor (1.4), ZE is the elasticity coefficient (150 for steel-bronze pairs), Zρ is the contact factor (2.8), and σH is the allowable contact stress (200 MPa). Substituting T2 = T1 · η · i = 55,110 · 0.65 · 50 = 1,791,075 N·mm, we get a ≥ 211.63 mm. After iterating, I selected m = 8 mm, q = 10 (diameter factor), and d1 = 140 mm, resulting in a practical center distance of 270 mm. The lead angle γ is computed as:
$$ \gamma = \tan^{-1}\left( \frac{z_1}{q} \right) = \tan^{-1}\left( \frac{1}{10} \right) \approx 3.27^\circ $$
which is below the self-locking threshold for the chosen materials. To verify structural integrity, I performed bending and rigidity checks. The bending stress σF is evaluated using:
$$ \sigma_F = \frac{1.53 \cdot K_A \cdot T_2}{d_1 \cdot d_2 \cdot m \cdot \cos \gamma} \cdot Y_{Fa2} $$
where YFa2 is the form factor (2.35 for zv ≈ 50). With d2 = m · z2 = 400 mm, σF ≈ 17.2 MPa, well below the allowable 32 MPa. For rigidity, the worm shaft deflection Y is constrained by:
$$ Y = \sqrt{ \left( \frac{F_{t1} \cdot l^3}{48 \cdot E \cdot I} \right)^2 + \left( \frac{F_{r1} \cdot l^3}{48 \cdot E \cdot I} \right)^2 } $$
where Ft1 and Fr1 are tangential and radial forces, l is the shaft length (360 mm), E is the modulus of elasticity (2.06 × 105 MPa), and I is the moment of inertia. Calculations yield Y ≈ 0.0023 mm, less than the permissible 0.14 mm, confirming adequate stiffness.
For the motor selection, the power requirement is determined by the input torque and speed. Using P = (n1 · T1) / 9550, with n1 = 1000 rpm and T1 = 55,110 N·mm, the minimum power is 5.8 kW. However, to account for losses and peak loads, I chose a Y160M-6 motor rated at 7.5 kW and 970 rpm, ensuring sufficient margin for marine operations. The integration of this motor with the worm gear system allows for smooth acceleration and deceleration, facilitated by the electromagnetic clutch and synchronizer. The clutch enables quick disengagement for self-locking, while the synchronizer manages gear shifts to maintain optimal ratios during chain handling.
The control system employs a PLC module with input/output modules for sensors monitoring oil level, chain position, and rotational speed. For example, the oil sensor triggers lubrication when viscosity changes, and the position sensor halts operation upon reaching limits. This automation reduces human intervention and enhances reliability. The table below summarizes the sensor specifications and their roles in the worm gear self-locking mechanism:
| Sensor Type | Parameter Monitored | Function in Worm Gear System |
|---|---|---|
| Oil Level Sensor | Lubricant Volume | Activates nozzle injection when levels drop |
| Position Sensor | Anchor Chain Position | Signals PLC to engage/disengage self-locking |
| Speed Sensor | Rotational Velocity | Adjusts gear ratio via synchronizer |
| Vibration Sensor | Dynamic Loads | Prevents unintended release under shock |
This comprehensive approach ensures that the worm gear self-locking device operates efficiently across various marine conditions. The dual-worm design not only doubles the locking force but also provides redundancy in case of component failure. Moreover, the PLC’s high-speed processing allows for real-time adjustments, making the system adaptable to sudden environmental changes like storms or strong currents.
In conclusion, my novel marine worm gear self-locking device addresses critical limitations of traditional systems by combining mechanical robustness with intelligent control. The design achieves reliable self-locking through optimized geometry and material selection, while the integration of sensors and PLCs enhances precision and safety. Future work will focus on refining the control algorithms, conducting full-scale sea trials, and exploring lightweight materials to reduce overall weight. This innovation has the potential to significantly improve anchoring operations in the maritime industry, reducing risks and operational costs. The worm gear mechanism, with its inherent self-locking properties, remains a cornerstone of this development, demonstrating how traditional engineering principles can be enhanced with modern technology for superior performance.
Throughout this project, I have emphasized the importance of iterative design and validation. The mathematical models and tables presented here provide a foundation for further optimization, and the incorporation of real-time monitoring sets a new standard for marine machinery. As vessels continue to face harsh environments, such advanced worm gear systems will play a pivotal role in ensuring safety and efficiency. I am confident that this design will inspire further innovations in marine propulsion and anchoring technologies, solidifying the worm gear’s place as a versatile and reliable component in engineering solutions.
