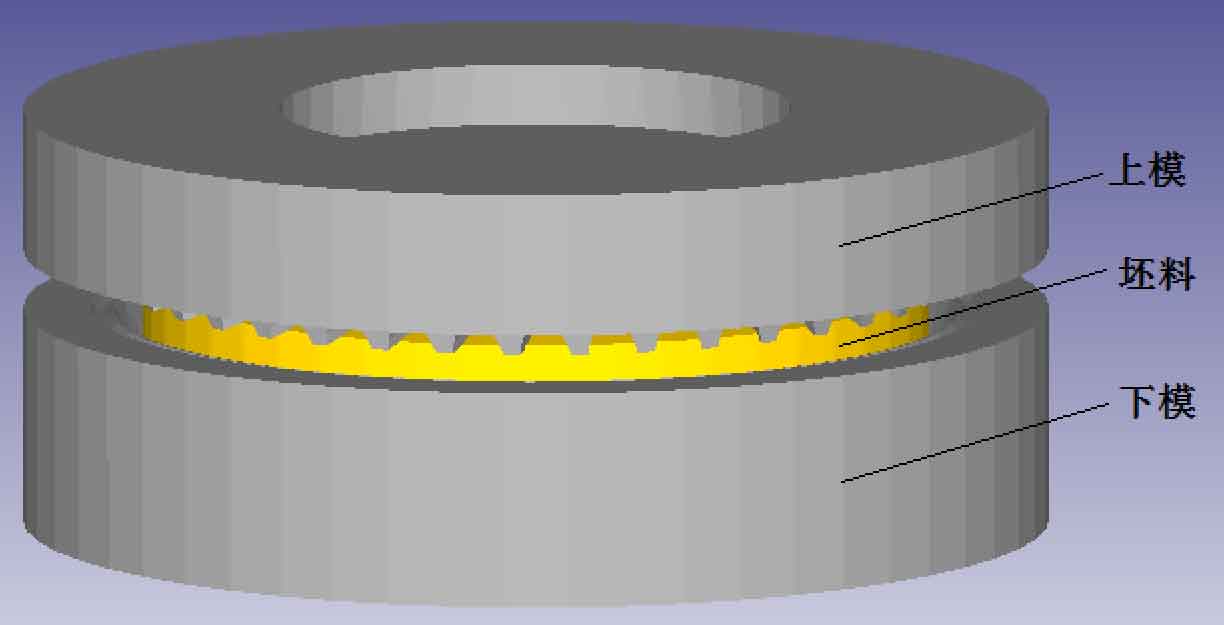
Using CATIA V5R21 three-dimensional mathematical modeling software, the three-dimensional mathematical models of upper and lower dies and blanks in the warm precision forging process of automobile rear axle driven spiral bevel gear are established and saved as STL format, and then the assembly file in STL format is imported into DEFORM-3D. The assembly drawing is shown in Figure 1. Enter the pre-processing interface of DEFORM-3D, and set the unit system to SI unit system (international standard unit system). Set the precision forging temperature of the blank as 800 ℃, set the grid division of the blank as 400000, set the preheating temperature of the upper and lower molds as 300 ℃, set the movement speed of the upper mold as 12.5 mm / s down along the Z axis, the material of the selected blank is 20MnCr5, which corresponds to steel Din-20MnCr5 in the material library of DEFORM-3D, the selected die material is 4Cr5MoSiV1, and die material H13 in the material library of DEFORM-3D, Set the friction coefficient as the friction coefficient of warm machining 0.25, generate the data file after checking, click Run after exiting to enter the simulation stage for numerical simulation calculation.
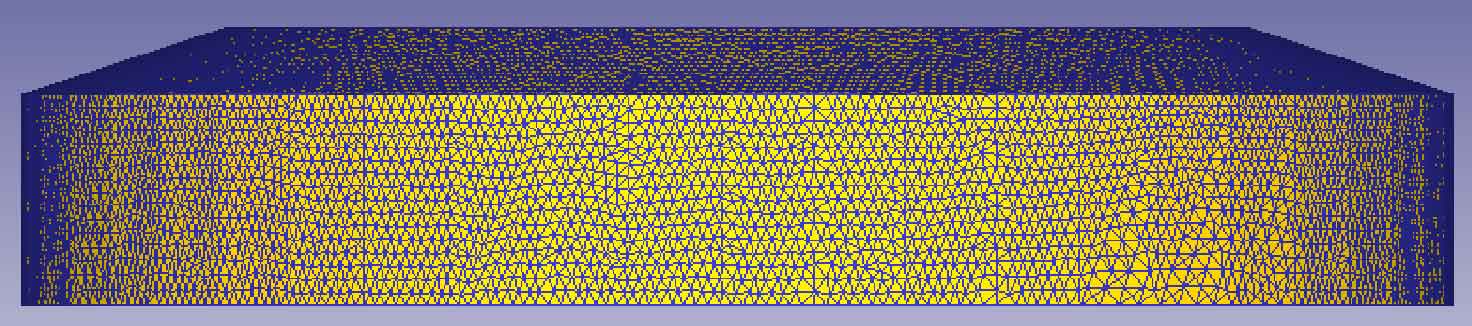
In the process of DEFORM-3D numerical simulation, because the plastic deformation process of metal will lead to the distortion of the divided grid, the grid will be re divided at each step in the whole simulation process, and the principle of grid re division is that the more prone the distortion is, that is, the position with large deformation. When the grid is re divided, the greater the grid density is, the smaller the grid is; For the part with small deformation, the mesh is not easy to be distorted. When re dividing the mesh, the smaller the mesh density, the larger the mesh.
Figure 2 is the grid distribution diagram of blank and forging, in which figure (a) is the grid distribution diagram of blank and figure (b) is the grid distribution diagram of forging. It can be seen from the figure that the grid distribution before forging processing is relatively uniform. As the upper die moves down, the grid distribution in the lower half of the spiral bevel gear is sparse and coarse, while the grid distribution at the top (tooth shaped part) of the spiral bevel gear is dense and fine. This shows that in the processing process, the deformation of the top (tooth shape part) of the spiral bevel gear is large, which is easy to produce mesh distortion. Therefore, the mesh is dense when the mesh is re divided, while the deformation of the lower half of the spiral bevel gear is small, the mesh is stable, and it is not easy to produce distortion.