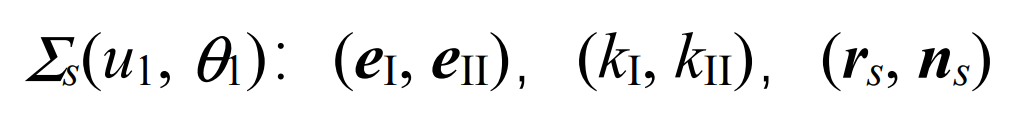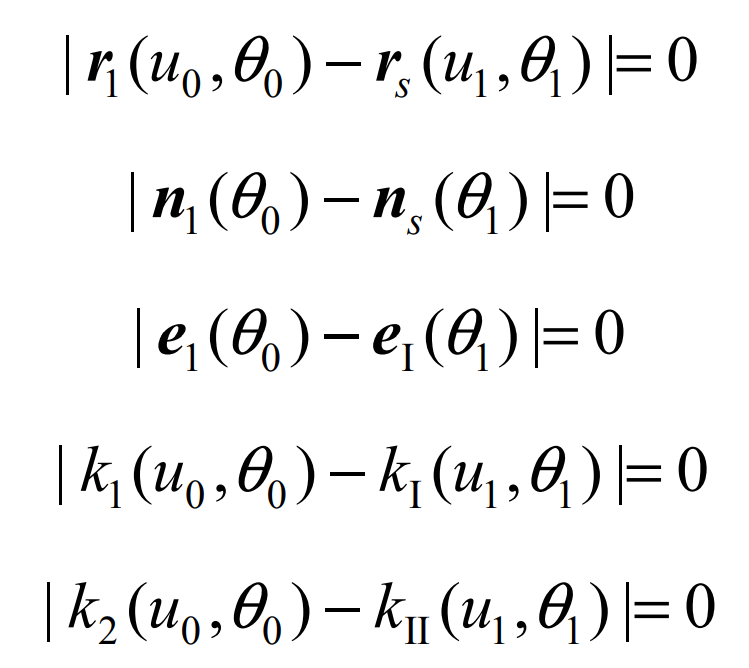The numerical differentiation method is used to calculate the numerical differentiation of the formula, calculate the main direction and main curvature of the spiral bevel gear pinion, and record the diameter vector and normal vector as follows:
The formula represents the same neighborhood of the same surface, so their geometric properties are exactly the same, that is, they meet the following requirements:
The above equation contains small wheel processing parameters (Sr1, Q1, γ M1, EM1, XG1), cutter head parameters (RP, α 1) , curve coordinate parameters (U1, θ 1) Nine nonlinear equations. The machining parameters of spiral bevel gear can be determined by solving the equations.
Before solving, some parameters can be determined first, such as the installation angle of wheel blank γ M1, cutterhead pressure angle α 1,Xb1=–Xg1sin γ m1。 Therefore, the actual parameters are 6.
The initial value and value range of the solution of the spiral bevel gear formula are relatively easy to determine, so the spiral bevel gear formula is suitable to be solved by the optimization method. An example calculation is completed by using the nonlinear constraint optimization method and the MATLAB optimization function fmincon.