This paper mainly analyzes the dynamic response model simulation case 1. That is to say, only the influence of gear meshing stiffness reduction on the dynamic response of gear system is considered. The influence of gear pitting failure on the time-varying meshing stiffness of gear system is calculated and analyzed, and the gear meshing stiffness is introduced into the gear dynamic model as the internal excitation of gear system, and the gear train with different gear states considering only the influence of stiffness excitation is obtained by Runge Kutta method The vibration response of driven gear along the meshing line is analyzed in time domain and frequency domain.
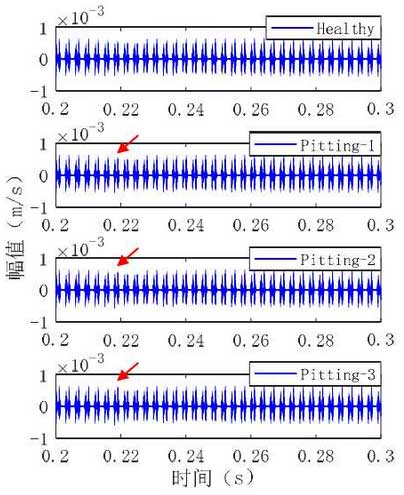
The duration of the vibration signal given in Fig. 1 is 0.1s, which is about half of the rotation period of the driven gear. In the case of only considering the influence of meshing stiffness reduction on the dynamic response of gear system, the relationship between pitting fault degree and vibration speed signal amplitude is explored according to figure 3-4. Under the condition of healthy gear, the time domain of vibration signal is relatively stable, and the amplitude of the signal is 0.00048 M / s. As indicated by the red arrow in Figure 1, the vibration response signal of pitting-1 and pitting-2 is not obvious, and the fault feature is relatively weak. The amplitude of pitting-1 and pitting-2 are 0.0005 / and 0.00054 / respectively. The amplitude of pitting-3 speed signal is 0.00058 ‰. Compared with the healthy gear, the signal amplitude of pitting-3 has obvious fluctuation, and the fault characteristics are relatively obvious.
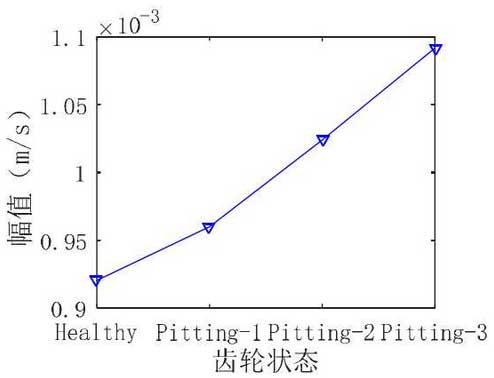
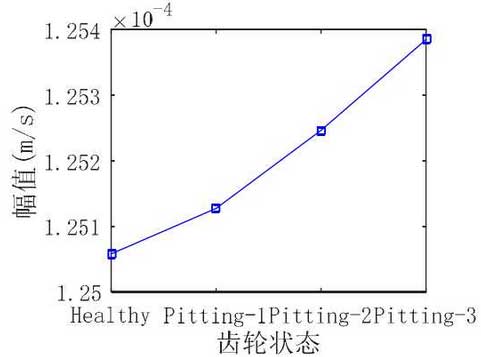
The RMS value and peak peak value of vibration speed signal in case I under different gear states are shown in Fig. 2 and Fig. 3 respectively. It can be seen that with the aggravation of gear pitting fault degree, RMS value and peak peak peak value almost increase linearly; when the gear pitting degree is the most serious, RMS value and peak peak peak value reach the maximum value; however, when the gear pitting reaches a certain degree, RMS value and peak peak peak value increase linearly Pitting-2 and pitting-3 increased faster than pitting-1.
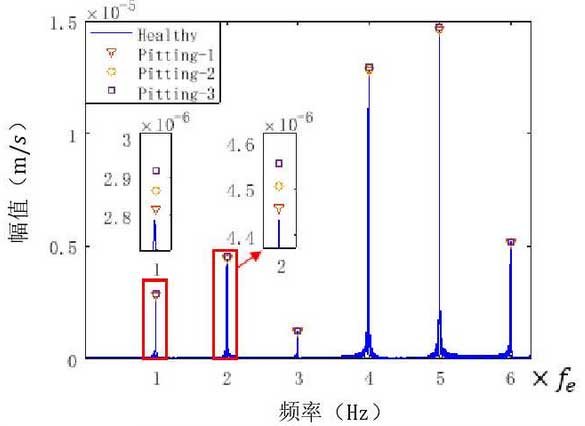
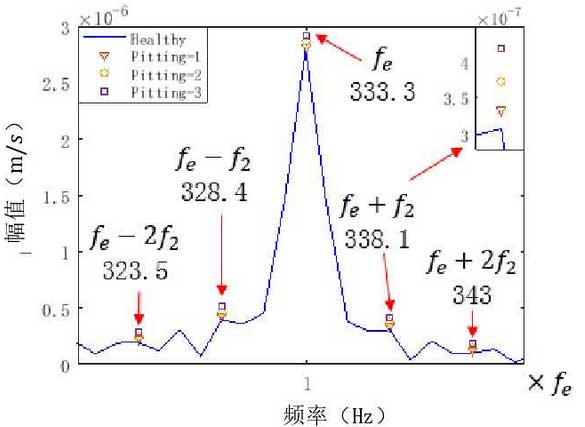
Next, the frequency spectrum of the vibration speed signal of the gear system is analyzed, in which Fe is the meshing frequency of the gear, 2Fe, 3Fe are the multiple frequency of the meshing frequency. Figure 4 shows the spectrum of the first six times of the meshing frequency of the vibration speed signal. The spectrum of the healthy gear only has the meshing frequency and its harmonic components. When the amplitudes of one and two meshing frequencies Fe and 2Fe are amplified locally, it is obvious that the amplitudes of one and two meshing frequencies Fe and 2Fe increase steadily with the aggravation of pitting failure compared with healthy gears. Through the analysis of higher meshing frequency, the higher harmonic of meshing frequency has the same characteristics. Fig. 5 shows a local enlarged view of the frequency component around the meshing frequency. With the occurrence of gear pitting fault, the sideband components around the meshing frequency will appear and increase significantly. The frequency difference between the side bands △ f = 4.9hz is approximately equal to the gear shaft rotation frequency f2 = 4.63hz. At the same time, the amplitude of these sidebands will increase steadily with the aggravation of gear pitting fault.