This paper presents an optimization methodology for reducing the volume of planetary gear systems in thin-seam shearer rocker arms while maintaining operational reliability. Focusing on NGW-type planetary transmission mechanisms, we establish a comprehensive mathematical model considering multiple constraints including gear strength requirements and planetary configuration conditions.
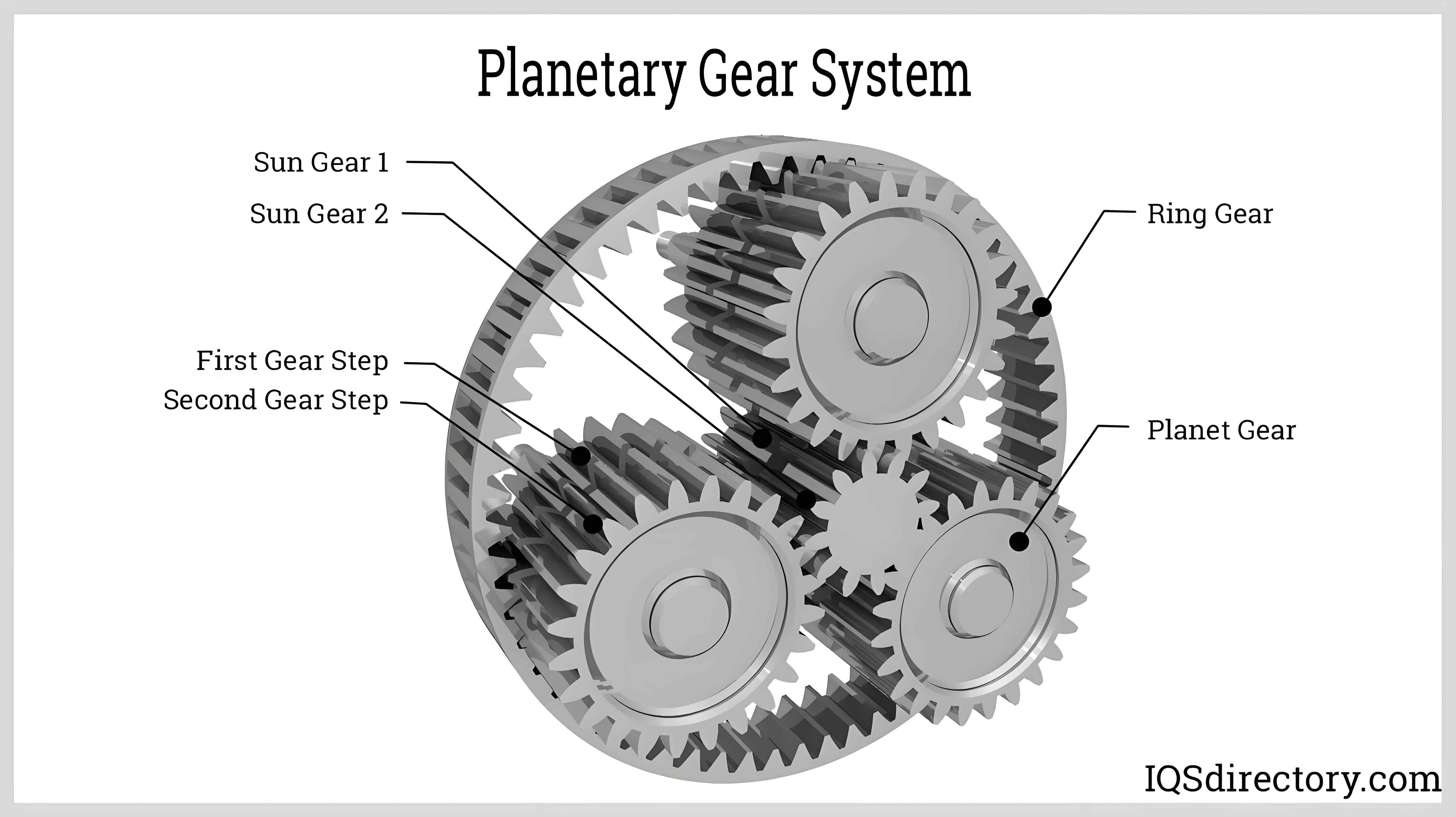
1. Mathematical Modeling
1.1 Design Variables
Five key parameters were selected as optimization variables:
$$ \mathbf{x} = [Z_a, Z_b, Z_c, b, m_n]^T $$
Where:
$Z_a$ = Sun gear teeth count
$Z_b$ = Ring gear teeth count
$Z_c$ = Planet gear teeth count
$b$ = Tooth width (mm)
$m_n$ = Module (mm)
1.2 Objective Function
Minimize total planetary gear system volume:
$$ f(\mathbf{x}) = \frac{\pi}{4}x_4^2\left[x_1^2 + x_3^2 + 4x_5^2\right]x_2 $$
Where $x_1$-$x_5$ correspond to the design variables in sequence.
1.3 Constraints
Key constraints for planetary gear optimization:
| Constraint Type | Mathematical Expression |
|---|---|
| Contact Stress | $$ \frac{766}{\sigma_{Hlim}}\sqrt[3]{\frac{T_aK_Ak_\beta(i+1)}{bd^2i}} \geq 1 $$ |
| Bending Stress | $$ \frac{12.6T_aK_Ak_\beta Y_F}{bm_n^2Z_a\sigma_{Flim}} \geq 1 $$ |
| Assembly Condition | $$ Z_a + Z_b = N \cdot C_s $$ |
| Adjacency Condition | $$ (Z_a + Z_c)\sin(\pi/C_s) > Z_c + 2 $$ |
2. Optimization Methodology
2.1 Nonlinear Programming Approach
The fmincon solver with sequential quadratic programming (SQP) was implemented with initial parameters:
$$ \mathbf{x}_0 = [17, 83, 33, 175, 9]^T $$
2.2 Genetic Algorithm Implementation
Key GA parameters for planetary gear optimization:
| Parameter | Value |
|---|---|
| Population Size | 500 |
| Crossover Probability | 0.8 |
| Mutation Probability | 0.1 |
| Generations | 500 |
3. Optimization Results
Comparative results of planetary gear optimization:
| Parameter | Initial | fmincon | GA |
|---|---|---|---|
| Sun Gear Teeth ($Z_a$) | 17 | 19 | 17 |
| Planet Gear Teeth ($Z_c$) | 33 | 31 | 31 |
| Ring Gear Teeth ($Z_b$) | 83 | 81 | 79 |
| Tooth Width (mm) | 175 | 171 | 172 |
| Module (mm) | 9 | 8 | 8 |
| System Volume (mm³) | 1.184×10⁸ | 9.254×10⁷ | 8.969×10⁷ |
| Volume Reduction | – | 21.8% | 24.3% |
4. Planetary Gear Performance Analysis
The optimized planet gear system demonstrates significant improvements:
$$ \Delta V_{GA} = \frac{V_{initial} – V_{GA}}{V_{initial}} \times 100\% = 24.3\% $$
Key contact stress reduction for planet gears:
$$ \sigma_H^{optimized} = 0.87\sigma_H^{initial} $$
5. Conclusion
This study demonstrates effective volume reduction strategies for planetary gear systems in thin-seam shearers. The genetic algorithm showed superior performance in finding global optima for planet gear configurations, achieving 24.3% volume reduction while maintaining required strength characteristics. The optimization framework provides valuable insights for high-power-density planetary gear design in constrained mining environments.
