It is known that the transmission mechanism of an automobile engine is a closed bevel gear transmission mechanism with 90 ° intersection angle. The power P1 transmitted by the small bevel gear is 9.2 kW, the speed n1 is 970 R / min, the transmission ratio I is 3, and the working condition factor K is 1.5. The material of bevel gear is 40Cr. After quenching and tempering, the Brinell hardness (HB) is 250. The material of large bevel gear is 35SiMn, Quenched and tempered, and the Brinell hardness (HB) is 230. It is required to optimize the design with the objective of minimizing the volume of bevel gear pair.
After sorting out and calculating the above parameters, the working torque T1 of driving bevel gear can be obtained as follows:
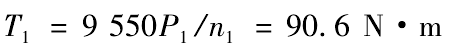
According to the material and metal technology specification of bevel gear transmission mechanism, it is found that the allowable contact stress of tooth surface [σ H] is 640 MPa and the allowable bending stress of tooth root [σ F] is 250 MPa.
Penalty function method is an indirect method to solve constrained optimization problems, which transforms constrained optimization problems into a series of unconstrained problems to solve without destroying the original constraints. In this paper, the constrained nonlinear programming problem is constructed as a fitness function val (x) by using the outer point method of penalty function method
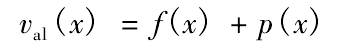
Where: F (x) is the objective function of the mathematical model; P (x) is the penalty term. For the problem of minimization, there are three aspects
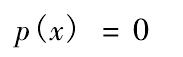
or
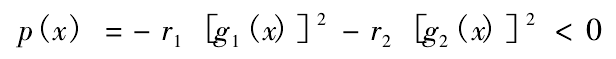
Where: R1 and R2 are penalty factors, which are positive number sequences increasing with the increase of iteration times.
The three-dimensional inequality constrained nonlinear objective problem in the formula is transformed into fitness function problem in the form of external penalty function, that is, the two performance constraints of the formula in the optimization design mathematical model are constructed as penalty terms in the fitness function, and then the boundary conditions of the design variables in the mathematical model are taken as the upper and lower bounds matrix of the variables in the genetic algorithm.
In this example, the bevel gear pair is a closed gear transmission with soft tooth surface. Combined with the bevel gear transmission algorithm, the penalty factor R1 of bevel gear tooth surface contact strength condition is taken as 1, and the penalty factor R2 of bevel gear tooth root bending strength condition is taken as 0.5.
Because the number of teeth of the driving bevel gear is small, the compound tooth shape factor is large in most cases, so the compound tooth shape factor should be used as the basis for calculating the bending strength of the tooth root of the bevel gear. In this example, the compound tooth shape factor can be taken as 4.80.
Using fmincon function of MATLAB optimization toolbox, data such as pitch circle diameter, tooth number ratio, cone distance, tooth width, objective function are input in the main program. Some key procedures of. M format file are as follows:


The running results of the main program are shown in the table
The results show that G1 (x) = – 0.081 MPa ≈ 0, G2 (x) = 247.591 1 MPa > 0. It can be seen that the optimal solution is located on the boundary of the tooth surface contact strength condition, and the bending strength of the tooth root is greatly improved.
The number of pinion teeth in the optimal solution is rounded to an integer value of 19, and then tested by the constraint conditions, G1 (x0) = 13.603 1 MPa > 0, G2 (x0) = 247.659 5 MPa > 0, which shows that the optimal solution is in the feasible region.

