The precise and efficient transmission of motion and force in advanced mechanical systems, such as robotics and aerospace mechanisms, often relies on specialized gearing solutions. Among these, the strain wave gear, also known as a harmonic drive, stands out for its unique operating principle and exceptional performance characteristics. The fundamental operation involves the controlled elastic deformation of a thin-walled flexible spline, typically called the flexspline, by a wave generator. This deformation allows for meshing with a rigid circular spline (circular spline), enabling high-ratio speed reduction within a compact package. The advantages of this configuration are significant, including high torque density, exceptional positional accuracy, minimal backlash, and quiet operation.
The performance envelope of a strain wave gear is intrinsically linked to the geometry of the teeth on both the flexspline and the generated conjugate profile on the circular spline. A critical design challenge is to avoid undesirable contact conditions, such as edge or point contact, which can lead to stress concentrations, accelerated wear, and reduced lifespan. The double-circular-arc (DCA) tooth profile for the flexspline has been identified as a highly effective solution to this problem. By comprising two circular arc segments connected by a common tangent, this profile promotes favorable line contact and improves load distribution across the tooth flank.
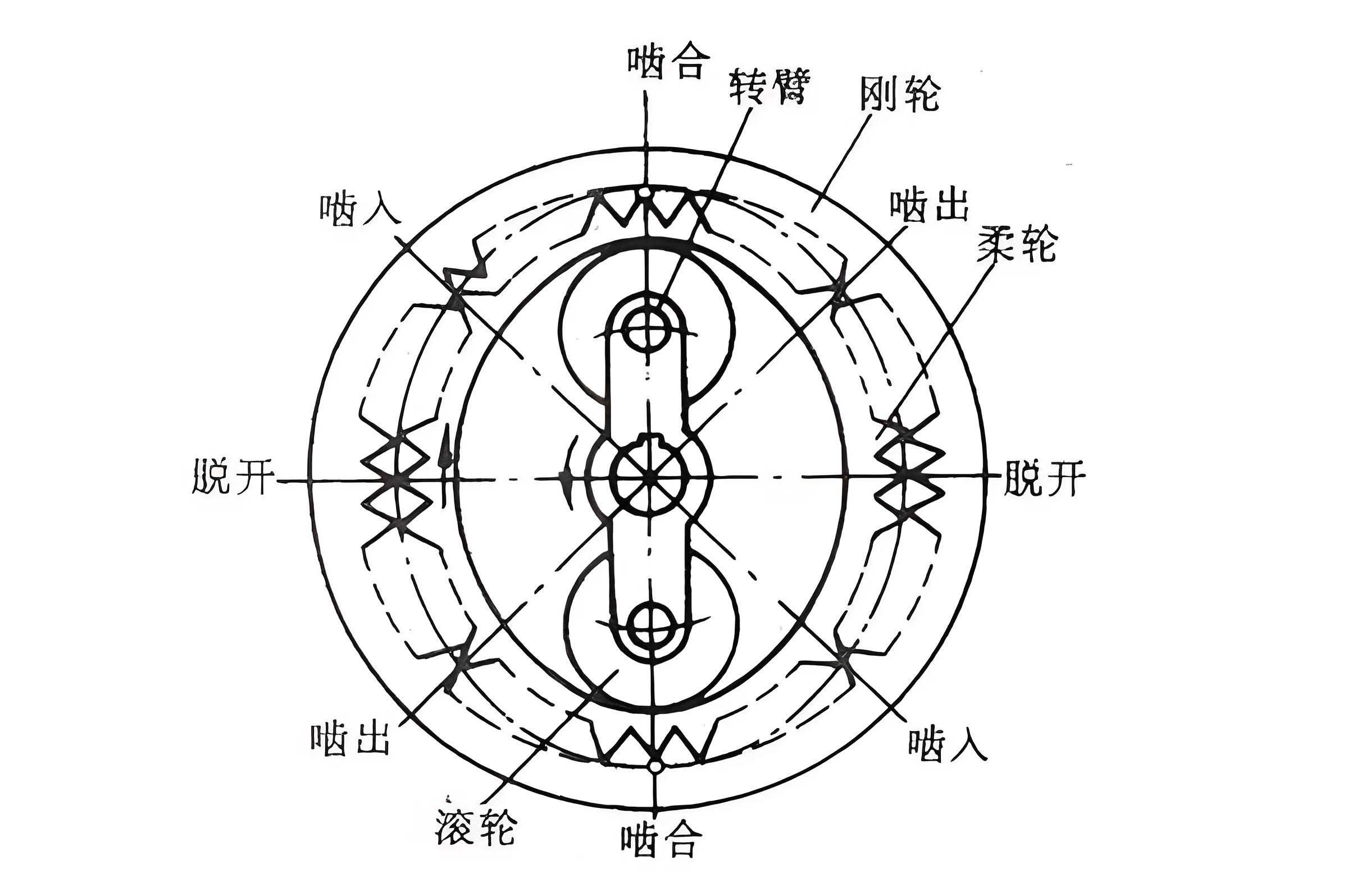
However, the superior performance of the DCA profile is not inherent but is highly dependent on the optimal selection of its geometric parameters. These parameters govern the conjugate action—the precise kinematic relationship that ensures continuous and proper contact between the flexspline and circular spline teeth throughout the engagement cycle. Suboptimal parameters can shrink the effective conjugate zone, create interference, or generate unfavorable contact stresses. Therefore, a systematic investigation into the influence of key DCA flexspline profile parameters on the conjugate characteristics is essential for advancing the design and performance of strain wave gear drives.
This analysis employs an exact conjugate theory based on a refined kinematic methodology. Unlike traditional approximate methods that rely on simplifications for the deformed flexspline contour, this approach utilizes a precise formulation that avoids integral approximations, leading to more accurate results. Using this theoretical foundation, the influence of primary DCA profile parameters—namely the convex arc radius, concave arc radius, common tangent length, common tangent inclination angle, and radial deformation coefficient—on the conjugate zone and the shape of the conjugate circular spline tooth profile is rigorously analyzed and quantified.
Mathematical Modeling and Coordinate System Definition
To analyze the meshing kinematics of the strain wave gear, a precise mathematical model must be established. The core of this model is the parametric definition of the DCA flexspline tooth profile and the coordinate transformations describing the motion of all components.
The DCA profile for a single flexspline tooth is constructed from three distinct segments: a convex circular arc near the tooth tip, a concave circular arc near the tooth root, and a straight line (common tangent) connecting them. A local coordinate system $\{O_1; X_1, Y_1\}$ is fixed to the flexspline tooth. The origin $O_1$ is located at the intersection of the tooth’s symmetry axis (the $Y_1$-axis) and the neutral curve of the non-deformed flexspline cylinder. The $X_1$-axis is tangent to this neutral curve at $O_1$. The profile is parameterized by the arc length $s$, starting from the tooth tip (Point A).
The equations for each segment in the local flexspline coordinate system are as follows:
1. Convex Arc Segment AB:
$$
\vec{r}_{AB}(s) = \begin{bmatrix}
\rho_a \cos(\alpha_a – s/\rho_a) + x_{Oa} \\
\rho_a \sin(\alpha_a – s/\rho_a) + y_{Oa} \\
1
\end{bmatrix}, \quad
\vec{n}_{AB}(s) = \begin{bmatrix}
\cos(\alpha_a – s/\rho_a) \\
\sin(\alpha_a – s/\rho_a) \\
1
\end{bmatrix}
$$
for $s \in (0, l_1)$, where $l_1 = \rho_a (\alpha_a – \delta_l)$.
Here, $\rho_a$ is the convex arc radius, $\alpha_a = \arcsin[(h_a + X_a)/\rho_a]$, $h_a$ is the addendum, $X_a$ is the convex arc center offset, $x_{Oa} = -l_a$, $y_{Oa} = h_f + d_s – X_a$, $h_f$ is the dedendum, $d_s$ is the distance from the root circle to the neutral layer, and $\delta_l$ is the common tangent inclination angle.
2. Common Tangent Segment BC:
$$
\vec{r}_{BC}(s) = \begin{bmatrix}
\rho_a \cos \delta_l + x_{Oa} + (s – l_1)\sin \delta_l \\
\rho_a \sin \delta_l + y_{Oa} – (s – l_1)\cos \delta_l \\
1
\end{bmatrix}, \quad
\vec{n}_{BC}(s) = \begin{bmatrix}
\cos \delta_l \\
\sin \delta_l \\
1
\end{bmatrix}
$$
for $s \in (l_1, l_2)$, where $l_2 = l_1 + (\rho_a + \rho_f)\tan \delta_l$.
3. Concave Arc Segment CD:
$$
\vec{r}_{CD}(s) = \begin{bmatrix}
x_{Of} – \rho_f \cos[\delta_l + (s – l_2)/\rho_f] \\
y_{Of} – \rho_f \sin[\delta_l + (s – l_2)/\rho_f] \\
1
\end{bmatrix}, \quad
\vec{n}_{CD}(s) = \begin{bmatrix}
\cos[\delta_l + (s – l_2)/\rho_f] \\
\sin[\delta_l + (s – l_2)/\rho_f] \\
1
\end{bmatrix}
$$
for $s \in (l_2, l_3)$, where $l_3 = l_2 + \rho_f \{ \arcsin[(X_f + h_f)/\rho_f] – \delta_l \}$.
Here, $\rho_f$ is the concave arc radius, $X_f$ is the concave arc center offset, $x_{Of} = \pi m/2 + l_f$, and $y_{Of} = h_f + d_s + X_f$.
To describe the assembly motion, a global fixed coordinate system $\{O_2; X_2, Y_2\}$ is attached to the circular spline, with its origin at the circular spline’s center. The moving coordinate system $\{O; X, Y\}$ is attached to the wave generator, with its axes aligned with the generator’s major and minor axes. The key kinematic variables are defined as follows:
| Symbol | Definition |
|---|---|
| $\phi$ | Rotation angle of the non-deformed flexspline end relative to a fixed reference. |
| $\phi_1$ | Angle parameter defining the position vector on the deformed flexspline neutral curve. |
| $\phi_2$ | Rotation angle of the wave generator. |
| $\gamma$ | Angle of the position vector for a point on the deformed flexspline neutral curve. |
| $\beta$ | Angle defining the orientation of the flexspline’s local coordinate system relative to the global system. |
| $\omega_0$ | Maximum radial deformation of the flexspline neutral curve. |
| $r_m$ | Radius of the non-deformed flexspline neutral curve. |
| $z_g$, $z_r$ | Number of teeth on the circular spline and flexspline, respectively. |
For a cosine cam wave generator, the polar equation of the deformed flexspline neutral curve is given by:
$$
\rho(\phi_1) = r_m + \omega(\phi_1) = r_m + \omega_0 \cos(\phi_1)
$$
The other essential kinematic relationships, taking $\phi_1$ as the independent variable for precision, are:
$$
\phi(\phi_1) = \frac{1}{r_m} \int_0^{\phi_1} \sqrt{\rho^2 + \left(\frac{d\rho}{d\phi_1}\right)^2} d\phi_1, \quad \phi_2 = \frac{z_r}{z_g} \phi
$$
$$
\gamma(\phi_1) = \phi_1 – \phi_2, \quad \mu(\phi_1) = \arctan\left( \frac{\rho}{d\rho/d\phi_1} \right), \quad \beta(\phi_1) = \gamma(\phi_1) + \mu(\phi_1)
$$
The derivatives $\gamma’$ and $\beta’$ are directly computed without integral approximations.
Exact Conjugate Theory Based on Refined Kinematics
The fundamental condition for conjugate motion between two surfaces is that their relative velocity at the point of contact has no component in the direction of the common normal. For the strain wave gear, this condition can be expressed in matrix form using a refined kinematic method. The coordinate transformation matrix from the flexspline system $S_1$ to the fixed circular spline system $S_2$ is:
$$
\mathbf{M}_{21}(\phi_1) = \begin{bmatrix}
\cos\beta(\phi_1) & \sin\beta(\phi_1) & \rho(\phi_1)\sin\gamma(\phi_1) \\
-\sin\beta(\phi_1) & \cos\beta(\phi_1) & \rho(\phi_1)\cos\gamma(\phi_1) \\
0 & 0 & 1
\end{bmatrix}
$$
The base vector transformation matrix is $\mathbf{W}_{21}$, which consists of the rotational part of $\mathbf{M}_{21}$.
The core of the exact conjugate theory is the meshing equation derived from the condition of continuous contact:
$$
\vec{n}^T \cdot \mathbf{B} \cdot \vec{r}_1 = 0
$$
where $\vec{n}$ and $\vec{r}_1$ are the unit normal vector and position vector of the flexspline tooth profile point in the $S_1$ system, respectively. The matrix $\mathbf{B}$ is the kinematic matrix, defined as:
$$
\mathbf{B}(\phi_1) = \mathbf{W}_{21}^T \frac{d\mathbf{M}_{21}}{d\phi_1} = \begin{bmatrix}
0 & \beta'(\phi_1) & \rho(\phi_1)\gamma'(\phi_1)\cos\mu(\phi_1) – \rho'(\phi_1)\sin\mu(\phi_1) \\
-\beta'(\phi_1) & 0 & \rho(\phi_1)\gamma'(\phi_1)\sin\mu(\phi_1) + \rho'(\phi_1)\cos\mu(\phi_1) \\
0 & 0 & 0
\end{bmatrix}
$$
The critical advantage of this formulation is that all elements of the $\mathbf{B}$ matrix are expressed using the derivatives of the explicitly defined functions $\beta(\phi_1)$, $\gamma(\phi_1)$, $\rho(\phi_1)$, and $\mu(\phi_1)$. This completely avoids the need for approximate integral solutions for $\phi_1$, which are common in traditional methods, thereby significantly improving computational accuracy.
For a given wave generator position defined by $\phi_1$, the meshing equation is a scalar equation with the flexspline arc length $s$ as the unknown. Solving this equation for $s$ yields the specific point on the flexspline tooth profile that is in conjugate contact at that instant. The corresponding conjugate point on the theoretical circular spline tooth profile is then obtained by the transformation:
$$
\vec{r}_2(\phi_1, s(\phi_1)) = \mathbf{M}_{21}(\phi_1) \cdot \vec{r}_1(s(\phi_1))
$$
By discretizing the parameter $\phi_1$ over its operational range (typically $0$ to $\pi$), a complete set of discrete points defining the conjugate circular spline tooth profile can be calculated.
Case Study: Conjugate Zone and Profile Analysis
To investigate the influence of DCA parameters, a specific case of a cup-type strain wave gear is analyzed. The primary design parameters are listed in the table below.
| Parameter Group | Symbol | Value |
|---|---|---|
| Gear Specifications | Module, $m$ | 0.38 mm |
| Flexspline Teeth, $z_r$ | 160 | |
| Circular Spline Teeth, $z_g$ | 162 | |
| Radial Deformation, $\omega_0$ | 0.38 mm | |
| DCA Profile Parameters | Convex Arc Radius, $\rho_a$ | 0.645 mm |
| Concave Arc Radius, $\rho_f$ | 0.70 mm | |
| Common Tangent Length, $h_l$ | 0.04 mm | |
| Common Tangent Inclination, $\delta_l$ | 13.0° | |
| Addendum, $h_a$ | 0.252 mm | |
| Dedendum, $h_f$ | 0.378 mm |
Applying the exact conjugate theory to this baseline configuration reveals important characteristics of the strain wave gear meshing. The solution of the meshing equation for the entire flexspline tooth profile yields a mapping between the flexspline arc length $s$ and the conjugate angle parameter $\phi_1$. This mapping, known as the Theoretical Conjugate Existent Domain (TCED), typically consists of two separate branches or zones for a DCA profile.
Zone 1 (Primary Conjugate Zone): This is the major zone of contact, corresponding to the primary load-bearing region during operation. For the baseline parameters, it spans an angular range of approximately $\phi_1 \in [16.63^\circ, 62.1^\circ]$. Within this zone, points from all three segments of the flexspline tooth (convex arc, common tangent, concave arc) find conjugate partners.
Zone 2 (Secondary Conjugate Zone): This is a smaller, secondary zone of potential contact. For the baseline, it exists in the range $\phi_1 \in [-0.072^\circ, 8.766^\circ]$. This zone is associated with a different kinematic configuration and typically involves contact on the concave arc segment of the flexspline.
Transforming the conjugate points from both zones yields two distinct theoretical tooth profiles for the circular spline: one generated from Zone 1 and another from Zone 2. In a practical strain wave gear design, only one continuous profile can be manufactured. The profile generated from the primary conjugate zone (Zone 1) is typically selected as the “effective conjugate profile” to avoid kinematic interference. A key design objective is to optimize the DCA parameters such that the secondary conjugate profile from Zone 2 aligns as closely as possible with the primary profile from Zone 1. This alignment effectively merges the two conjugate zones, maximizing the total arc length of contact and significantly improving the load-sharing capability and smoothness of the strain wave gear transmission.
Parametric Influence on Conjugate Characteristics
The conjugate zone and the resulting circular spline tooth profile are sensitive functions of the DCA flexspline parameters. The following analysis systematically varies each key parameter while holding others constant at their baseline values to isolate its effect.
1. Influence of Convex Arc Radius ($\rho_a$)
The convex arc radius primarily influences the tip region of the flexspline tooth. Its variation shows a distinct effect.
| Aspect | Influence of Increasing $\rho_a$ |
|---|---|
| Conjugate Zone (TCED) | The entire conjugate zone shifts along the negative flexspline arc length ($s$) axis. The angular range ($\phi_1$ span) and width of the zone remain virtually unchanged. |
| Conjugate Profile (TCTP) | The conjugate profile generated from the flexspline’s convex arc translates along the positive X-direction in the circular spline coordinate system, but its shape is preserved. The conjugate profiles generated from the other flexspline segments are unaffected. |
Mathematically, for the conjugate profile segment derived from the flexspline convex arc, the shift $\Delta X$ is approximately proportional to the change in the profile parameter $x_{Oa}$, which is a function of $\rho_a$ and $l_a$: $\Delta X \propto f(\Delta \rho_a)$.
2. Influence of Concave Arc Radius ($\rho_f$)
The concave arc radius governs the geometry near the tooth root of the flexspline. Its effect is more pronounced on the conjugate dynamics.
| Aspect | Influence of Increasing $\rho_f$ |
|---|---|
| Conjugate Zone (TCED) | For the primary zone (Zone 1), the angular range decreases while the associated flexspline arc length also decreases. For the secondary zone (Zone 2), the angular range increases. Both zones shift towards a central arc length value, effectively moving closer together. |
| Conjugate Profile (TCTP) | The conjugate profile generated from the flexspline’s concave arc translates along the negative X-direction. Its shape remains constant. The conjugate profiles from other segments are unaffected. |
The relationship can be described by the change in the parameter $x_{Of}$, leading to a profile shift: $\Delta X_{\text{concave}} \propto -g(\Delta \rho_f)$.
3. Influence of Common Tangent Length ($h_l$)
The length of the common tangent connector primarily affects the mid-section of the tooth profile.
| Aspect | Influence of Increasing $h_l$ |
|---|---|
| Conjugate Zone (TCED) | The conjugate region corresponding to the flexspline convex arc is unaffected. The region corresponding to the flexspline concave arc shifts along the positive flexspline arc length ($s$) axis. The angular range ($\phi_1$) for this region remains constant. |
| Conjugate Profile (TCTP) | All segments of the conjugate circular spline tooth profile remain unchanged in both shape and position. The parameter $h_l$ influences the transition point between segments on the flexspline but does not alter the fundamental geometry of the circular arcs themselves, hence the conjugate profile is invariant to $h_l$ changes. |
The invariance of the TCTP is because the coordinate transformation and meshing condition operate on the circular arc and straight line geometries directly, which are defined independently of $h_l$ once the transition points $l_1$ and $l_2$ are accounted for in the domain of $s$.
4. Influence of Common Tangent Inclination Angle ($\delta_l$)
The inclination angle defines the slope connecting the two arcs and plays a crucial role in bridging the conjugate zones.
| Aspect | Influence of Increasing $\delta_l$ |
|---|---|
| Conjugate Zone (TCED) | The conjugate region for the flexspline convex arc is unaffected. For the primary zone (Zone 1) related to the concave arc, the angular range increases while the associated flexspline arc length decreases. For the secondary zone (Zone 2) related to the concave arc, both the angular range and the associated flexspline arc length decrease. |
| Conjugate Profile (TCTP) | Similar to $h_l$, the conjugate tooth profile shape and position are not directly altered by changes in $\delta_l$. Its main effect is kinematic, altering the mapping between $s$ and $\phi_1$ for the connecting region. |
The angular span of Zone 1, $\Delta \phi_{1,\text{zone1}}$, can be expressed as a function of $\delta_l$ and other fixed parameters: $\Delta \phi_{1,\text{zone1}} \approx \Phi(\delta_l; \rho_a, \rho_f, \omega_0)$.
5. Influence of Radial Deformation Coefficient ($\omega_0$)
This is a fundamental operational parameter of the strain wave gear, defining the amplitude of the wave generator.
| Aspect | Influence of Increasing $\omega_0$ |
|---|---|
| Conjugate Zone (TCED) | For the primary zone (Zone 1), the angular range increases while the width of the zone (in $\phi_1$) decreases; the associated flexspline arc length remains constant. For the secondary zone (Zone 2), both the angular range and the zone width decrease, while its associated flexspline arc length remains constant. |
| Conjugate Profile (TCTP) | The conjugate profile generated from the flexspline convex arc rotates clockwise about a virtual pivot point, maintaining its shape. The two conjugate profile segments generated from the flexspline concave arc (from Zone 1 and Zone 2) move closer together, also preserving their shape. |
The rotation of the convex arc conjugate profile is directly linked to the change in the kinematic angle $\beta(\phi_1)$, which is a strong function of $\omega_0$: $\Delta \beta \propto \frac{\partial \beta}{\partial \omega_0} \Delta \omega_0$. The convergence of the two concave arc conjugate profiles is critical for optimizing the total contact ratio in the strain wave gear.
Discussion and Design Implications
The parametric analysis reveals clear strategies for optimizing the double-circular-arc tooth profile in strain wave gear drives. The primary design goal is to maximize the effective conjugate zone—the continuous range of engagement where smooth, interference-free contact occurs. This directly translates to higher load capacity, better stress distribution, and smoother torque transmission.
The analysis shows that parameters like the common tangent length ($h_l$) and inclination ($\delta_l$) have a predominant effect on the kinematic mapping—the size and location of the conjugate zones on the flexspline arc length coordinate. They are crucial for “tuning” the engagement intervals. In contrast, the arc radii ($\rho_a$, $\rho_f$) and the radial deformation ($\omega_0$) have a more direct influence on the physical shape and position of the conjugate circular spline tooth profile itself.
A key optimization pathway identified is the strategic adjustment of $\rho_f$ and $\omega_0$. As these parameters increase, the two separate conjugate profiles generated from the flexspline concave arc (one from the primary zone and one from the secondary zone) converge. If parameters are selected such that these two profiles precisely coincide or overlap within an acceptable tolerance, a significant design improvement is achieved. This coincidence effectively merges the secondary conjugate zone into the primary one, creating a single, broader, and more robust zone of continuous conjugate action. This expanded conjugate zone means that a greater number of teeth are in simultaneous, proper contact at any given instant during the operation of the strain wave gear.
Furthermore, the use of the exact conjugate theory based on the independent variable $\phi_1$ provides a more reliable foundation for this optimization than traditional approximate methods. It eliminates errors associated with simplifying the flexspline deformation kinematics, ensuring that the predicted conjugate profiles and zones are accurate. This accuracy is paramount when pushing the performance limits of strain wave gear drives in demanding applications.
Conclusion
This investigation into the influence of double-circular-arc flexspline tooth profile parameters on the conjugate characteristics of strain wave gear drives yields several important conclusions for designers and engineers.
First, the precise mathematical modeling based on an exact kinematic theory, using the deformed flexspline angle $\phi_1$ as the fundamental variable, provides a accurate and efficient framework for analyzing strain wave gear conjugation. This method avoids the inaccuracies inherent in traditional approximate integral solutions, leading to more reliable predictions of the conjugate zone and tooth profile geometry.
Second, the parametric study elucidates distinct roles for different DCA profile parameters. The convex and concave arc radii ($\rho_a$, $\rho_f$) and the radial deformation coefficient ($\omega_0$) are primary drivers determining the shape and spatial orientation of the conjugate circular spline tooth profile. Meanwhile, the common tangent parameters ($h_l$, $\delta_l$) are key influencers of the kinematic conjugate zone’s extent and location on the flexspline tooth flank.
Third, a central finding is the potential to significantly enhance strain wave gear performance through parameter optimization. By carefully selecting values for $\rho_f$ and $\omega_0$, designers can engineer the convergence of the secondary conjugate tooth profile with the primary one. This strategic alignment functionally expands the total conjugate engagement zone, leading to a greater number of teeth in simultaneous contact. The result is a direct improvement in the strain wave gear’s torque capacity, load distribution, structural rigidity, and operational smoothness.
In summary, the double-circular-arc tooth profile represents a sophisticated and effective design for strain wave gear drives. Its full potential, however, is unlocked only through a deep understanding and deliberate optimization of its geometric parameters in relation to the exact conjugate kinematics of the system. The insights and methodology presented here provide a clear pathway for advancing the design of high-performance, reliable strain wave gear transmissions for the most challenging technological applications.
