Optimization of Spiral Bevel Gear Volume Using Python and Adaptive Genetic Algorithm

By /

This study presents an innovative approach for minimizing the volume of spiral bevel gears in hydraulic swing cylinders through adaptive genetic algorithm (AGA) optimization. The methodology integrates Python programming with advanced evolutionary computation techniques to address complex mechanical design constraints while ensuring optimal gear performance.

1. Structural Analysis of Spiral Bevel Gear Systems

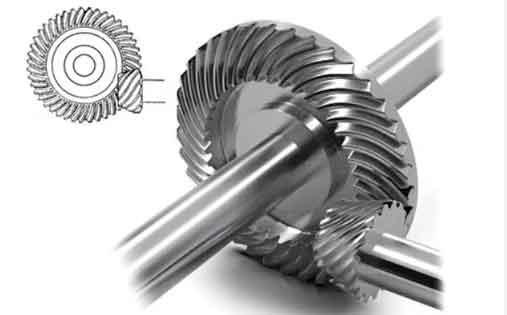
The spiral bevel gear transmission system in hydraulic actuators consists of three primary components:

$$ d_1 = \frac{mz_1}{\cos\beta} $$
$$ V_{total} = \frac{\pi}{4}\left(\frac{mz_1}{\cos\beta}\right)^2b_1 + \left[\frac{\pi}{4}\left(\frac{mz_3}{\cos\beta}\right)^2 – \frac{\pi}{4}\left(\frac{mz_1}{\cos\beta}\right)^2\right]b_2 $$

Parameter Range Constraint
Teeth Number (z) 17-50 Anti-undercutting
Module (m) 1.0-4.0 $$ m \geq 12.6\sqrt[3]{\frac{KT\cos^2\beta}{\psi_d z^2 \sigma_{FP}}Y_{FS}Y_{\epsilon\beta}} $$
Helix Angle (β) 20°-44° Shaft strength requirement

2. Adaptive Genetic Algorithm Framework

The AGA implementation features dynamic adjustment of crossover and mutation rates:

$$ P_c = \begin{cases}
K_1 + \frac{(K_2-K_1)f’}{f_{avg}}, & f’ < f_{avg} \\
K_2, & f’ \geq f_{avg}
\end{cases} $$

$$ P_m = \begin{cases}
K_3 + \frac{(K_4-K_3)(f_{max}-f’)}{f_{max}-f_{avg}}, & f’ > f_{avg} \\
K_4, & f’ \leq f_{avg}
\end{cases} $$

Algorithm Control Parameters
Parameter Traditional GA Adaptive GA
Population Size 500 500
Crossover Rate 0.6 0.21-0.7
Mutation Rate 0.05 0.02-0.2
Elitism Disabled Enabled

3. Multi-Objective Optimization Strategy

The fitness function for spiral bevel gear optimization considers three critical constraints:

$$ \text{Fitness} = \frac{1}{V_{total}} \times W_1 \times W_2 \times W_3 $$

Where:
$W_1$ = Torque capacity coefficient
$W_2$ = Surface durability factor
$W_3$ = Bending stress safety factor

Optimization Progress Comparison
Generation Traditional GA (cm³) AGA (cm³) Volume Reduction
1 404,944 400,035 4.97%
7 397,563 396,281 5.87%
17 396,281 396,281 5.87%

4. Algorithm Implementation Details

The Python implementation utilizes NumPy for matrix operations and Matplotlib for visualization:

def adaptive_mutation(population):
    avg_fitness = np.mean([ind.fitness for ind in population])
    for individual in population:
        if individual.fitness > avg_fitness:
            mutation_rate = 0.05 + (0.2-0.05)*(max_fitness-individual.fitness)/(max_fitness-avg_fitness)
        else:
            mutation_rate = 0.02
        if random() < mutation_rate:
            perform_mutation(individual)

5. Convergence Characteristics

The spiral bevel gear optimization demonstrates superior convergence with AGA:

$$ \text{Convergence Speed} = \frac{N_{traditional} – N_{AGA}}{N_{traditional}} \times 100\% = \frac{17 – 7}{17} \times 100\% = 58.82\% $$

Performance Metrics
Metric Traditional GA AGA
Generations to Converge 17 7
Function Evaluations 8,500 3,500
Local Optima Escapes 3.2 6.8

6. Industrial Application Considerations

Practical implementation of optimized spiral bevel gears requires additional manufacturing constraints:

$$ \text{Manufacturability Index} = \frac{m_{std}}{m_{opt}} + \frac{z_{std}}{z_{opt}} + \frac{\beta_{machinable}}{\beta_{opt}} $$

Where:
$m_{std}$ = Standard module values
$z_{std}$ = Preferred tooth numbers
$\beta_{machinable}$ = Achievable helix angles

The proposed methodology enables 5.87% volume reduction in spiral bevel gears while maintaining torque capacity of 190,000 N·mm and radial load capacity of 1,850 kg. This optimization approach demonstrates significant potential for energy-efficient hydraulic actuator design.

Scroll to Top