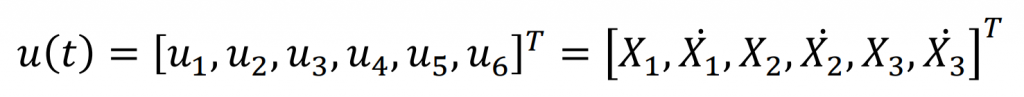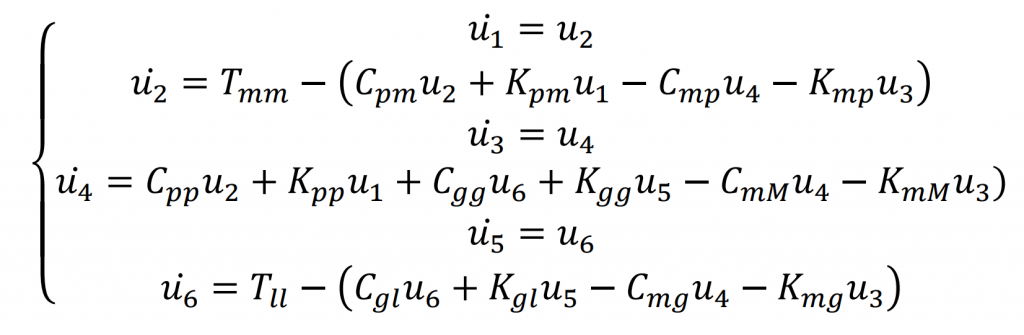The variable step adaptive Runge Kutta numerical integration method will be used to solve the nonlinear dynamic differential equation of bevel gear system. Firstly, the order of the equation needs to be reduced and the state vector u is introduced. Its representative meaning is as follows:
In this way, the equation can be transformed into:
To solve the equation, you can directly call the differential equation solving function in MATLAB software, such as ode45 function. In this paper, Runge Kutta numerical method is used to solve the equations. The gear dynamic equation is an initial value problem, so the calculation speed and success or failure of the calculation largely depend on whether the selection of the initial value of the integral is reasonable. For similar gear dynamics equations, there are generally three initial value schemes:
a) The initial displacement and initial speed are both taken as zero, which corresponds to the transient state of the central bevel gear system when starting from the static state. Through such initial value selection, the transient response of the system can be obtained, but it is difficult to obtain the steady-state response of the system;
b) The initial displacement is determined by static deformation, and the initial velocity is taken as zero. This initial static deformation is close to the elastic deformation of the steady-state vibration of the body system. The initial speed is zero, shaving the rigid body rotation component in the system, leaving the vibration component, which is very suitable for solving the steady-state response of the bevel gear dynamic system;
c) The initial displacement is determined by the static deformation, and the initial speed is determined by the theoretical speed of the system. This initial value scheme is close to the stable operation state of bevel gear and can solve the steady-state response of the system, but the numerical integration process is often unstable due to the excessive initial speed.
To sum up, the second initial value scheme will be adopted in this paper. The initial conditions are determined as follows:
The time history of each variable in the equation can be obtained by Runge Kutta method and numerical method. Through the analysis of the time history diagram, the system response type can be preliminarily determined. Then, the properties of the nonlinear dynamic system are obtained by combining the phase plane diagram and FFT spectrum analysis diagram.
Phase plane method, also known as geometric method, is a qualitative analysis method, which can obtain some important properties of the system without solving differential equations. The method of phase plane diagram is to project any state variable (x, x) onto R2 plane. Through the phase plan, the motion period, equilibrium state and stability of the system can be obtained directly. If the motion of the system is periodic, the trace on the phase plane is a closed curve; If it has quasi periodic property, the trace on the phase plane is a closed curve band with a certain width; If the system is chaotic, the trace on the phase plane does not fill the phase plane regularly.
Fast Fourier transform spectrum analysis (FFT) is to obtain the amplitude spectrum by Fourier analysis of the time history of the system response, which can determine the behavior of the system response. The vertical bar discrete spectrum in the form of separation corresponds to the periodic vibration of the system, and the height of the spectral line corresponds to the intensity of the vibration. If the system is quasi periodic, there will be a pair of fundamental frequencies and the linear combination of these fundamental frequencies in the amplitude spectrum. For the chaotic system, the amplitude spectrum has a certain continuity in a wide frequency band.
The above methods will be used to analyze the dynamic characteristics of the central bevel gear of an aeroengine.