The design of worm gear drives is a fundamental yet complex task in mechanical engineering. These components are indispensable for transmitting motion and power between non-intersecting, perpendicular shafts, offering distinct advantages such as high single-stage reduction ratios, compactness, smooth operation, and inherent self-locking capability. Their application spans across various industries, from automotive steering systems to heavy industrial machinery and precision instruments. However, the traditional manual design process for worm gear drives is often time-consuming, iterative, and prone to human error. It involves intricate calculations for sizing, extensive material selection based on tribological properties, rigorous strength and wear checks, and finally, detailed three-dimensional modeling. This complexity directly impacts product development cycles.
To address these challenges, this article presents a comprehensive framework for a parametric design system focused on worm gear drives. The core philosophy is to leverage parameterization and feature-based modeling to automate the entire workflow—from initial sizing based on service conditions to the final generation of accurate 3D CAD models. By formalizing the design logic, material databases, and geometric relationships, the system aims to liberate engineers from repetitive calculations, minimize errors, and significantly accelerate the design process. The implementation is demonstrated using SolidWorks as the modeling platform and Visual Basic for Applications (VBA) for creating a custom interface and automating the modeling steps via SolidWorks API (Application Programming Interface). The resulting system not only streamlines design but also creates a digital foundation for subsequent simulation (FEA, kinematics) and manufacturing preparation.
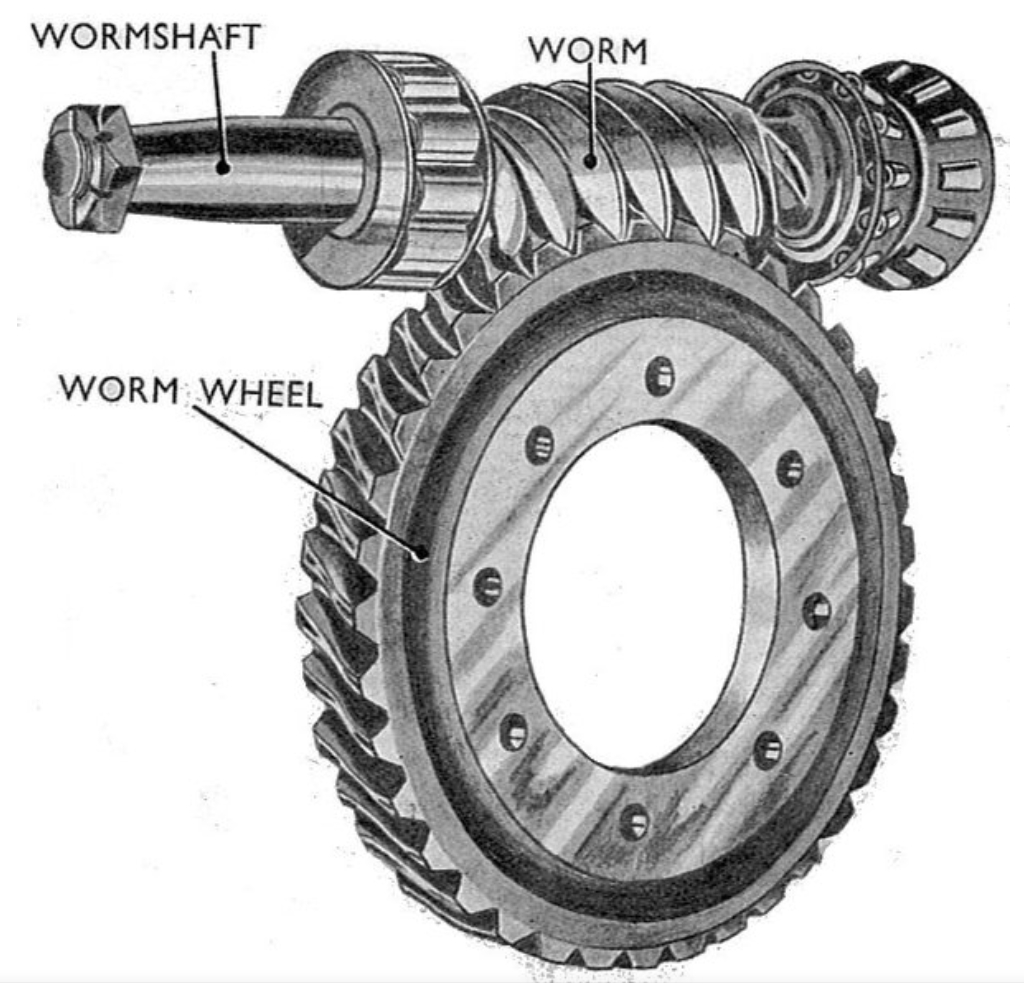
Foundations of Worm Gear Drive Design
The design of a reliable worm gear drive begins with a clear understanding of the operational requirements and the underlying failure modes. The designer must first establish a set of primary input parameters that uniquely define the drive’s geometry and performance.
Design Input Parameters and Material Selection
The initial phase involves gathering all necessary application data. These parameters form the basis for all subsequent calculations and are typically specified by the product’s functional needs.
| Parameter Category | Typical Parameters |
|---|---|
| Operational Load | Input power (P), input speed (n1), output torque (T2), duty cycle, load characteristic (steady, shock, etc.) |
| Kinematic Requirements | Desired gear ratio (i), rotational direction, efficiency target |
| Life and Reliability | Required service life (in hours), safety factors, operating environment |
Material selection is critical due to the high sliding friction inherent in worm gear drive operation. The primary failure mechanisms are wear, scoring (adhesive wear), and pitting fatigue. To mitigate these, the worm and worm wheel are typically made from dissimilar materials with favorable tribological properties. The worm, being the harder, fewer component, is usually made of case-hardened, induction-hardened, or nitrided steel. The worm wheel, which experiences more wear, is commonly made from bronze or cast iron alloys. Common pairings include:
- Worm: 16MnCr5, 20MnCr5 (case-hardened), 42CrMo4 (induction-hardened).
- Worm Wheel: Tin Bronze (e.g., CuSn12Ni), Aluminum Bronze (e.g., CuAl10Ni5Fe4), Gray Cast Iron (GGG).
Design Methodology and Automated Workflow
The design logic for a worm gear drive depends on whether it operates in a closed (lubricated) or open (unlubricated) housing. For the more common closed drives, pitting resistance (contact stress) is the primary design criterion, followed by checks for bending strength and worm shaft deflection.
The core design equation for the contact stress on the worm gear drive teeth is derived from the Hertzian contact theory and is given by:
$$
\sigma_H = Z_E \sqrt{\frac{9 K T_2}{a^3}} \geq [\sigma_H]
$$
Where:
- $\sigma_H$ is the calculated contact stress.
- $Z_E$ is the elastic coefficient of the material pair.
- $K$ is the load factor (accounts for dynamic load, load distribution).
- $T_2$ is the torque on the worm wheel.
- $a$ is the center distance.
- $[\sigma_H]$ is the allowable contact stress for the worm wheel material.
From this equation, the required center distance $a$ can be preliminarily determined. The center distance is the most critical overall dimension for a worm gear drive. The design process then proceeds to select standardized module ($m$) and worm diameter factor ($q$) or directly the worm reference diameter ($d_1$) to satisfy the center distance and strength requirements. Other key geometric parameters are derived subsequently:
- Number of worm threads ($z_1$) and worm wheel teeth ($z_2 = i \cdot z_1$).
- Wheel face width ($b_2$).
- Worm thread length ($L$).
- Lead angle ($\gamma = \arctan(z_1 m / d_1)$).
The automated workflow implemented in the parametric system mirrors this logic, as shown in the following sequence:
- Input & Initialization: User inputs operational parameters and selects materials from an integrated database.
- Preliminary Sizing: The system calculates a minimum required center distance $a’$ using the contact stress formula.
- Parameter Selection: The system selects a standard module $m$ and worm reference diameter $d_1$ from a lookup table that satisfies $a’$ and geometric constraints (e.g., $q = d_1 / m$ within recommended range).
- Geometric Calculation: All other dimensions (pitch diameters, tip diameters, root diameters, lengths) are calculated automatically.
- Verification Loops: The system performs automated checks for bending stress $\sigma_F$ and worm shaft deflection $y$. If checks fail, the system iteratively adjusts key parameters (e.g., selects a larger module or center distance) and recalculates.
- Final Output: Upon passing all checks, a final, validated set of geometric parameters is produced for modeling.
Parametric Modeling of Worm Gear Drive Components
With the final dimensions from the design stage, the next phase is the automatic generation of 3D solid models. This is achieved by programming the modeling sequence using the SolidWorks API. The modeling strategy for the worm and the worm wheel differs due to their distinct geometries.
Worm (ZA Profile) Modeling
For a common ZA (Archimedean) profile worm, the thread profile in the axial section is a straight-sided trapezoid. The worm thread is essentially a screw thread with this profile. The coordinates for the trapezoidal tooth space in the axial plane are critical for sketching. Given the axial module $m_x$, pressure angle $\alpha$, worm reference diameter $d_1$, tip diameter $d_{a1}$, and root diameter $d_{f1}$, the profile vertices (see conceptual sketch) can be defined parametrically. Let $p_x = \pi m_x$ be the axial pitch. The coordinates for one side of the symmetric profile are:
$$
\begin{aligned}
P_1 &= (p_x/4 – (d_{a1} – d_1)\tan(\alpha)/2,\; d_{a1}/2) \\
P_2 &= (p_x/4 + (d_1 – d_{f1})\tan(\alpha)/2,\; d_{f1}/2) \\
P_3 &= (-p_x/4 + (d_1 – d_{f1})\tan(\alpha)/2,\; d_{f1}/2) \\
P_4 &= (-p_x/4 – (d_{a1} – d_1)\tan(\alpha)/2,\; d_{a1}/2)
\end{aligned}
$$
The modeling sequence in the automated system is:
- Create Worm Blank: Extrude a cylinder of diameter $d_{a1}$ and length equal to the thread length $L$.
- Create Helix Path: Create an Archimedean helix on the cylinder’s surface with a pitch equal to the lead $P_z = z_1 \cdot p_x$ and height $L$.
- Create Profile Sketch: On a plane through the axis, sketch the trapezoidal profile using the calculated coordinates.
- Cut Sweep: Perform a swept cut using the profile sketch as the contour and the helix as the path. This creates one thread groove.
- Circular Pattern: For a multi-start worm, pattern the cut sweep feature around the axis $z_1$ times with an angular increment of $360/z_1$ degrees.
- Add Features: Model shaft extensions, bearings seats, etc., based on additional parametric rules.
Worm Wheel Modeling
The worm wheel is essentially a helical gear with a throat shaped to envelop the worm. The key challenge is generating the involute tooth profile. The parametric equations for an involute curve in the Cartesian plane are fundamental. For a wheel with pressure angle $\alpha$, module $m$, and number of teeth $z_2$:
- Base circle diameter: $d_b = m z_2 \cos(\alpha)$
- Base circle radius: $r_b = d_b / 2$
The parametric equations for an involute starting at the base circle on the X-axis are:
$$
\begin{aligned}
x(\theta) &= r_b (\cos(\theta) + \theta \sin(\theta)) \\
y(\theta) &= r_b (\sin(\theta) – \theta \cos(\theta))
\end{aligned}
$$
Where $\theta$ is the roll angle (in radians). To create a tooth space, two mirrored involute segments are needed, spaced by the base circle tooth thickness. The modeling sequence is:
- Create Wheel Blank: Extrude a cylinder for the wheel rim based on the throat diameter and face width $b_2$.
- Create Throat: Revolve-cut the internal throat profile to match the worm’s tip diameter plus clearance.
- Generate Involute Curve Programmatically: The VBA code calculates a series of $(x, y)$ points using the involute equations for a defined $\theta$ range. These points are fed to SolidWorks API to create a spline, forming one flank of a tooth.
- Create Tooth Space Sketch: Mirror the involute spline, connect them with root and tip arcs based on $d_{f2}$ and $d_{a2}$, to form a closed profile of one tooth space.
- Create Helical Path: Create a helix on the wheel’s pitch cylinder with a lead angle $\gamma$ (matching the worm’s).
- Cut Sweep: Perform a swept cut using the tooth space sketch and the helical path.
- Circular Pattern: Pattern the tooth space cut $z_2$ times around the wheel axis to complete the gear teeth.
- Add Features: Add hub, web, keyway, etc.
System Implementation and Integration
The parametric design system is implemented as a standalone application or an add-in within SolidWorks. A graphical user interface (GUI) built with VBA forms serves as the central control panel. The interface is logically divided into sections:
- Input Panel: For entering operational power, speed, ratio, life, and selecting materials from dropdown lists linked to a material property database.
- Design Calculation Panel: Displays intermediate calculated values (required center distance, selected module, etc.) and allows for manual override of certain parameters if needed.
- Verification Results Panel: Shows the results of the contact stress, bending stress, and deflection checks with clear pass/fail indicators.
- Geometric Output Panel: Lists all final dimensions of the worm gear drive ($a$, $m$, $z_1$, $z_2$, $d_1$, $d_2$, $d_{a1}$, $d_{a2}$, etc.).
- Modeling Control Buttons: Buttons to execute the automatic generation of the worm part, the worm wheel part, and an assembly.
The VBA code behind this form orchestrates the entire process. It contains:
- Mathematical functions for all design calculations.
- Lookup tables for standard modules, diameter factors, and material properties.
- A library of SolidWorks API macros that perform specific modeling tasks (e.g., `CreateExtrusion`, `CreateHelix`, `CreateSweptCut`).
When the user clicks “Calculate & Verify,” the code runs the design logic. If verification passes, the parameters are stored. Clicking “Model Worm” then executes a script that launches SolidWorks (if not open), creates a new part, and calls the API functions in sequence, passing the stored parameters (like $d_1$, $m$, $z_1$, $L$) to build the worm model step-by-step as described earlier. The same process occurs for the worm wheel. This seamless integration between the design logic and the CAD environment is the cornerstone of the system’s efficiency.
Design Example and System Output
To demonstrate the system’s capability, consider designing a closed ZA-type worm gear drive for a conveyor system. The input conditions are:
| Parameter | Value |
|---|---|
| Input Power (P) | 9 kW |
| Worm Speed (n1) | 1440 rpm |
| Gear Ratio (i) | 57 |
| Service Life | 12,000 hours |
| Duty Cycle | 8 hours/day, steady load |
Using the system, the material pair selected is case-hardened steel (16MnCr5) for the worm and tin bronze (CuSn12Ni) for the wheel. After running the automated design and verification routine, the system produces the following key results:
| Design Parameter | Calculated Value |
|---|---|
| Center Distance (a) | 180 mm |
| Axial Module (mx) | 6.3 mm |
| Worm Ref. Diameter (d1) | 63 mm |
| Number of Worm Threads (z1) | 2 |
| Number of Wheel Teeth (z2) | 114 |
| Lead Angle (γ) | 11.31° |
| Wheel Face Width (b2) | 50 mm |
| Contact Stress (σH) | 245 MPa (≤ Allowable 280 MPa) PASS |
| Bending Stress (σF) | 32 MPa (≤ Allowable 45 MPa) PASS |
Upon confirming these results, the user can directly generate the 3D models. The system executes the modeling scripts, resulting in precise solid models of the worm and the worm wheel. These models are fully associative to the design parameters; changing a key parameter like the center distance in the input form and re-running the process would automatically regenerate new, dimensionally accurate models. This direct linkage ensures design consistency and enables rapid “what-if” analysis.
Conclusion
The development and implementation of a parametric design system for worm gear drives represent a significant step forward in modern mechanical design methodology. This system effectively bridges the gap between theoretical design calculations and practical, manufacturable CAD geometry. By encapsulating expert knowledge, standardized procedures, and material data into an automated workflow, it delivers substantial benefits:
- Enhanced Efficiency: It reduces design time from hours or days to minutes by automating calculations and model generation.
- Improved Accuracy: It eliminates manual calculation errors and ensures that all geometric relationships and design rules are strictly adhered to.
- Knowledge Management: It serves as a repository for design standards and best practices for worm gear drive design.
- Foundation for Digital Thread: The parameter-driven models provide a perfect starting point for further digital engineering activities, such as finite element analysis for stress verification, computational fluid dynamics for thermal analysis of the gearbox, and the generation of CNC code for manufacturing.
While the presented framework uses specific tools (SolidWorks, VBA), the underlying concept is universally applicable. The system can be extended by integrating more advanced optimization algorithms for weight or cost minimization, connecting to a broader PDM/PLM system, or incorporating more complex worm profiles (e.g., ZI, ZN). In conclusion, the parametric design system transforms the worm gear drive design process from a manual, sequential task into an integrated, automated, and highly reliable engineering activity, directly contributing to shorter product development cycles and more robust mechanical designs.
