As an engineer specializing in mechanical transmission systems, I have extensively studied various types of screw gears, and I am excited to share insights on a innovative design: the planar double-enveloping toroidal worm gear drive. This reduction apparatus represents a significant advancement over traditional Archimedean screw gears, offering superior performance in terms of efficiency, load capacity, smooth operation, and longevity. In this article, I will delve into the principles, characteristics, and advantages of this novel screw gear system, supported by detailed tables, formulas, and analysis. The term “screw gears” will be frequently emphasized to highlight its relevance in power transmission applications.
The planar double-enveloping worm gear reducer is a new type of transmission device that has garnered attention in industries such as construction, hoisting, chemical, and metallurgical machinery. Compared to conventional Archimedean screw gears, it exhibits remarkable benefits, which I will explore through technical comparisons. One key aspect is its enhanced meshing behavior due to the double-enveloping process, leading to improved durability and reliability. Throughout this discussion, I will refer to these components as screw gears to underscore their role in efficient motion control.
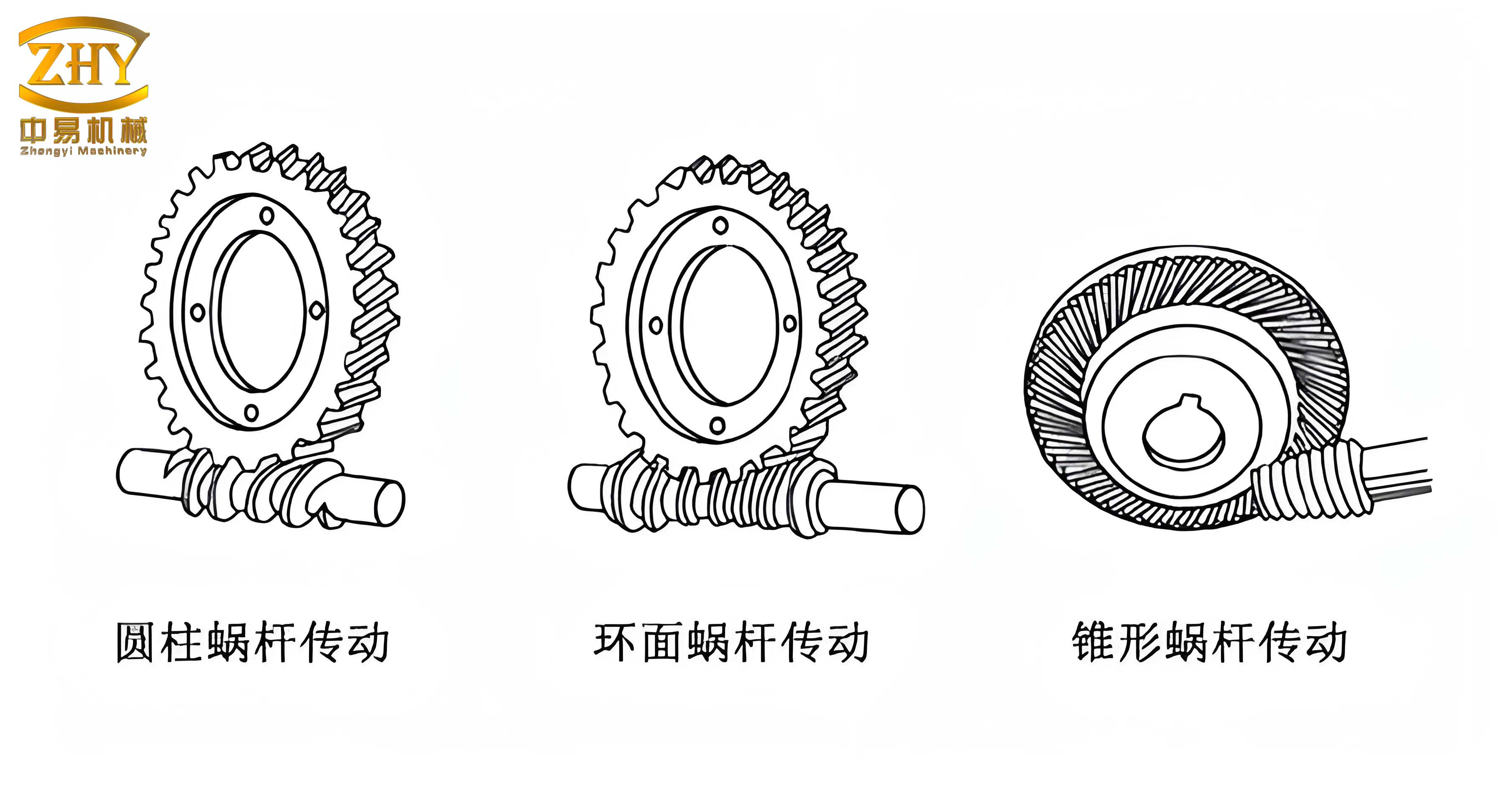
To understand the superiority of planar double-enveloping screw gears, let’s first examine their fundamental design. The worm gear pair is characterized by a worm whose tooth surface is generated by enveloping a plane, referred to as the generating plane. This process involves the plane rotating around a base circle, thereby enveloping the tooth profile. In manufacturing, this is achieved using a cutting tool or grinding wheel that mimics the plane. The double-enveloping method entails two stages: first, the worm is produced by single-enveloping with a plane, and then a hob tool, generated similarly, is used to cut the worm wheel. This results in a concave tooth surface on the worm wheel that matches the convex surface of the worm, ensuring optimal contact. This geometry is pivotal for the performance of screw gears in high-load scenarios.
The primary advantages of planar double-enveloping screw gears can be summarized into three key areas: large overlap ratio and high load capacity, excellent lubrication properties and efficiency, and large comprehensive curvature radius enhancing strength. I will elaborate on each with formulas and data. For instance, the overlap ratio, which indicates the number of teeth in contact simultaneously, is critical for load distribution. In planar double-enveloping screw gears, this ratio can exceed 2, doubling that of Archimedean screw gears. This is quantified by the formula for overlap ratio $\epsilon$: $$ \epsilon = \frac{L_c}{p_b} $$ where $L_c$ is the total contact line length and $p_b$ is the base pitch. For planar double-enveloping screw gears, $L_c$ is significantly increased due to the toroidal shape, leading to $\epsilon \geq 2$, compared to $\epsilon \approx 1$ for Archimedean screw gears. This directly translates to higher load capacity, as stress is distributed over more teeth.
To provide a clear comparison, I have compiled a table detailing the performance metrics between planar double-enveloping screw gears and Archimedean screw gears. This table underscores why screw gears of the double-enveloping type are preferred in demanding applications.
| Parameter | Planar Double-Enveloping Screw Gears | Archimedean Screw Gears |
|---|---|---|
| Transmission Efficiency | High (typically 85-95%) | Moderate (70-85%) |
| Torque Capacity | Up to 3 times higher | Base reference |
| Load Carrying Ability | Enhanced due to multiple tooth contact | Limited by single-tooth contact |
| Meshing Backlash | Minimal, ensuring precise motion | Relatively larger, affecting accuracy |
| Service Life | Long, due to reduced wear | Shorter, prone to wear and tear |
The efficiency of screw gears is a crucial factor in energy-saving applications. For planar double-enveloping screw gears, the efficiency $\eta$ can be modeled using the formula: $$ \eta = \frac{\tan(\gamma)}{\tan(\gamma + \phi)} $$ where $\gamma$ is the lead angle of the worm and $\phi$ is the friction angle. Due to the favorable lubrication conditions, $\phi$ is reduced, leading to higher $\eta$. In contrast, Archimedean screw gears often suffer from poor lubrication, increasing $\phi$ and lowering efficiency. The lubrication angle $\theta$, defined as the angle between the contact line and the relative velocity vector, plays a vital role. For planar double-enveloping screw gears, $\theta$ is large, promoting the formation of hydrodynamic oil films. This can be expressed as: $$ \theta = \arccos\left(\frac{\mathbf{v}_r \cdot \mathbf{t}_c}{|\mathbf{v}_r| |\mathbf{t}_c|}\right) $$ where $\mathbf{v}_r$ is the relative velocity and $\mathbf{t}_c$ is the tangent vector along the contact line. A larger $\theta$ enhances oil wedge effects, reducing friction and wear in screw gears.
Another significant aspect is the comprehensive curvature radius, which affects contact stress and thus load capacity. According to Hertzian contact theory, the contact stress $\sigma_H$ for screw gears is given by: $$ \sigma_H = \sqrt{\frac{F_n E^*}{\pi \rho_c}} $$ where $F_n$ is the normal load, $E^*$ is the equivalent Young’s modulus, and $\rho_c$ is the comprehensive curvature radius. For planar double-enveloping screw gears, $\rho_c$ is substantially larger—often 2 to 3 times that of Archimedean screw gears—due to the convex-concave mating. This reduces $\sigma_H$, allowing higher loads without failure. Specifically, the curvature radius ratio can be derived from the geometry: $$ \rho_c = \frac{\rho_w \rho_g}{\rho_w + \rho_g} $$ where $\rho_w$ and $\rho_g$ are the curvature radii of the worm and gear teeth, respectively. In double-enveloping screw gears, these radii are optimized through the enveloping process.
The manufacturing process of planar double-enveloping screw gears involves precise kinematics. The generating plane, denoted as $\Pi$, is tangent to the base circle in the worm’s axial section. During cutting or grinding, the plane rotates around the axis with a specific motion relationship, enveloping the tooth surface. This can be described by parametric equations. Let the generating plane be defined by: $$ \mathbf{r}(u,v) = \mathbf{r}_0 + u\mathbf{a} + v\mathbf{b} $$ where $\mathbf{r}_0$ is a reference point, $\mathbf{a}$ and $\mathbf{b}$ are direction vectors. As the plane rotates about the axis with angle $\theta$, the enveloped surface of the worm is given by: $$ \mathbf{R}(u,v,\theta) = \mathbf{T}(\theta) \cdot \mathbf{r}(u,v) $$ with $\mathbf{T}(\theta)$ being the rotation matrix. This mathematical representation ensures accurate generation of screw gears with minimal errors.
In practical applications, screw gears like these are subjected to dynamic loads. The dynamic load capacity can be assessed using the formula: $$ F_d = C_a \cdot F_n $$ where $C_a$ is the application factor, typically higher for double-enveloping screw gears due to their shock absorption. Moreover, the thermal performance is critical. The heat generation $Q$ in screw gears is related to friction: $$ Q = \mu F_n v_s $$ where $\mu$ is the coefficient of friction and $v_s$ is the sliding velocity. With better lubrication, $\mu$ is lower in planar double-enveloping screw gears, reducing $Q$ and enhancing thermal stability. This aligns with the need for efficient cooling systems, as referenced in auxiliary components like coolers, but here we focus on the screw gears themselves.
To further illustrate the benefits, consider the lifespan estimation. The service life $L_h$ of screw gears can be expressed as: $$ L_h = \frac{C^p}{F_n^p} \cdot \frac{10^6}{60 n} $$ where $C$ is the dynamic load rating, $p$ is the life exponent (e.g., 3 for point contact), and $n$ is the rotational speed. Due to higher $C$ and reduced $F_n$ from load sharing, planar double-enveloping screw gears exhibit longer $L_h$, often doubling that of Archimedean types. This makes them ideal for continuous operation in harsh environments.
In terms of design optimization, several parameters influence the performance of screw gears. These include the module $m$, number of worm threads $z_1$, gear teeth $z_2$, and center distance $a$. The gear ratio $i$ is: $$ i = \frac{z_2}{z_1} $$ For planar double-enveloping screw gears, $z_1$ is often kept low (e.g., 1-3) to achieve high ratios while maintaining efficiency. The contact pattern can be analyzed using simulation tools, ensuring that the screw gears operate within safe limits. Additionally, backlash control is vital for precision. The backlash $j$ can be minimized by adjusting the machining tolerance: $$ j = j_0 + \Delta j $$ where $j_0$ is the inherent backlash and $\Delta j$ is the variation. With double-enveloping, $j_0$ is inherently smaller, contributing to smoother motion in screw gears.
The application of planar double-enveloping screw gears extends across various industries. In construction machinery, they provide reliable reduction for hoists and conveyors. In chemical plants, they ensure safe operation under corrosive conditions. The compact structure of these screw gears allows for space-saving designs, which is crucial in mobile equipment. For example, the torque transmission capability can be calculated as: $$ T = F_t \cdot r_g $$ where $F_t$ is the tangential force and $r_g$ is the gear pitch radius. With higher load capacity, these screw gears can transmit more torque in the same envelope, reducing overall system weight.
From a maintenance perspective, screw gears require proper lubrication. The lubricant viscosity $\eta_l$ should be selected based on the sliding speed: $$ \eta_l = k \cdot v_s^{-0.5} $$ where $k$ is a constant. For planar double-enveloping screw gears, the concave tooth surface acts as an oil reservoir, promoting lubricant retention and extending oil change intervals. This feature is absent in Archimedean screw gears, leading to more frequent maintenance. Therefore, the total cost of ownership is lower for double-enveloping screw gears, despite higher initial investment.
To summarize the technical superiority, I have derived a comprehensive formula for the overall performance index $P$ of screw gears: $$ P = \eta \cdot \frac{\epsilon \cdot \rho_c}{j} $$ where higher $P$ indicates better performance. For planar double-enveloping screw gears, $P$ is significantly elevated due to high $\eta$, $\epsilon$, $\rho_c$, and low $j$. This index can guide engineers in selecting screw gears for specific applications. Moreover, ongoing research focuses on material advancements, such as using hardened steels or composites, to further enhance the durability of screw gears.
In conclusion, planar double-enveloping screw gears represent a groundbreaking innovation in reduction drive technology. Their design leverages geometric principles to achieve unmatched efficiency, load capacity, and longevity. Through detailed analysis using tables and formulas, I have demonstrated why these screw gears are superior to traditional Archimedean screw gears. As industries demand more reliable and efficient transmission systems, the adoption of planar double-enveloping screw gears is poised to grow, offering sustainable solutions for future mechanical designs. I encourage further exploration and implementation of these screw gears in diverse applications to harness their full potential.
