1. Establishment of finite element model
Several key problems in the establishment of finite element model include the selection of element type, the control of mesh size, the density of mesh division, the order of element, etc. Set the average cell side length to 2mm, and select the grid division method as automatic division. The material of spiral bevel gear is 20CrMnTi with elastic modulus E=2 07 × 105MPa, Poisson’s ratio μ = 0. 254, material density 7830kg/m3.
2. Create contact pairs
Under a certain working load, keeping the contact ratio of Gleason spiral bevel gear within a reasonable range can make the change of gear tooth stiffness relatively soft, and reduce the risk of vibration noise and strength failure caused by spiral bevel gear.
The contact ratio calculation formula of spiral bevel gear under full load is:
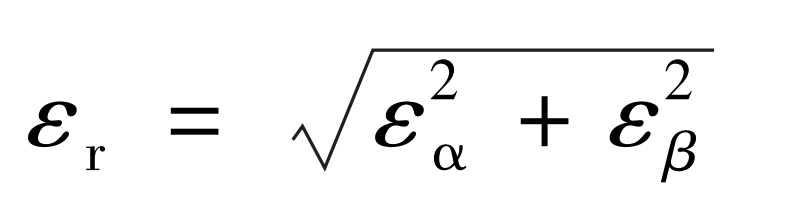
In the formula: ε r、 εα 、εβ They are total coincidence, end coincidence and longitudinal coincidence.
The coincidence of spiral bevel gear pair is 2 3. According to the requirement of coincidence degree, the maximum number of tooth pairs of spiral bevel gears engaged simultaneously is 3, so the three-tooth meshing model is adopted for contact modal analysis. The contact of spiral bevel gear adopts the solid model as face contact. Set three pairs of contact pairs, of which the big gear is the driving wheel as the contact surface, and the small gear is the driven wheel as the target unit, and the friction coefficient is 0 06。
3. Constraints and loading
In this paper, the free mode and contact mode of spiral bevel gears are analyzed respectively. The former does not require any constraints and loads on the model, while the contact mode analysis is much more complex than the former. According to the actual working conditions, apply 2100N · m torque on the input shaft and 890N · m resistance torque on the main shaft. The cylindrical constraint is imposed on the bearing, which makes the spiral bevel gear only rotate around the axis of the bearing.
