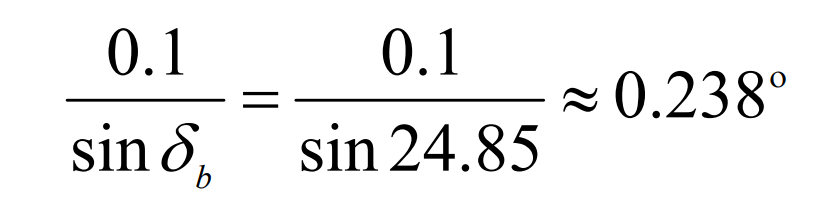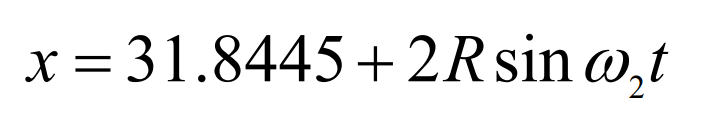According to the analysis of cutting motion of spiral bevel gear, the three linkage motions required in the process of bevel gear milling are: the rotation of gear blank (the speed is) ω 1) The gear blank rotates around the spindle of the horizontal rotary table (the speed is ω 2) And the movement of the gear blank along the boundary between the adjustment area and the cutting area (the speed is v); Corresponding to a-axis rotation, c-axis rotation and X-axis movement respectively. In order to cut the tooth surface of spiral bevel gear correctly, the relationship between the three speeds must meet the formula. It is preset that the rotation angle of C axis between two adjacent steps of the program compiled in the absolute coordinate system is 0.1 °. Then the rotation angle of axis a between two adjacent steps can be obtained according to the formula as follows:
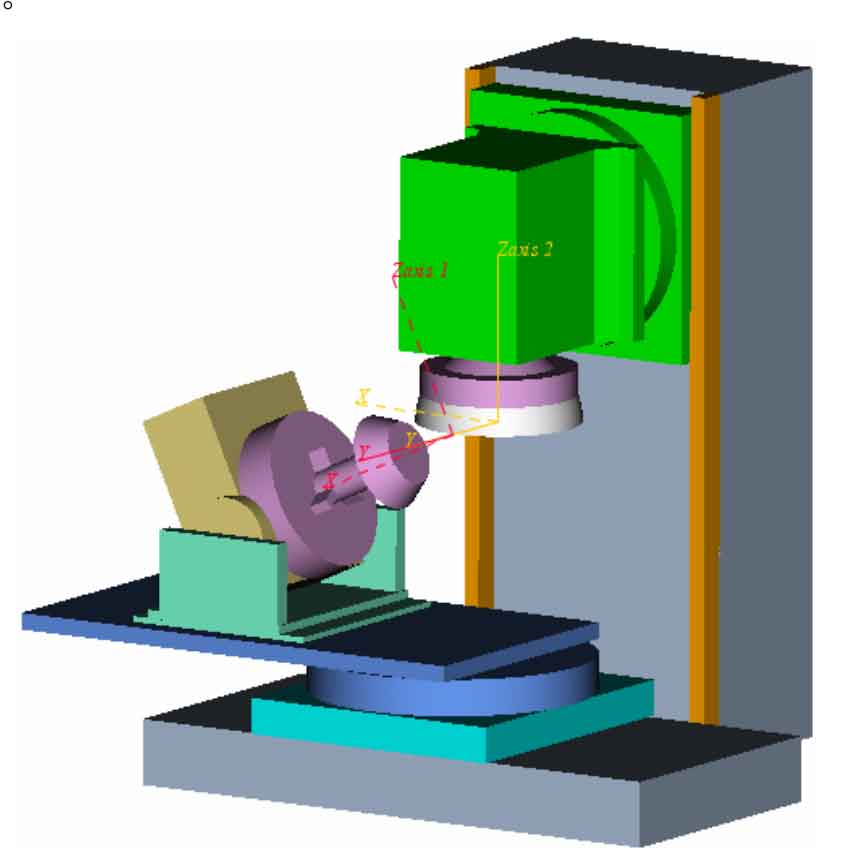
Because in the absolute coordinate system G90, each step of the NC machining program controls the absolute position coordinates of each moving axis, the movement of the gear blank in the x-axis direction can be realized by controlling the absolute position of the gear blank on the x-axis. The coordinate systems axis1 and Axis2 are established in the model of VERICUT spiral bevel gear cutting machine tool. Axis 1 is attached to the tooth blank model and is located at the cone apex of the tooth blank base cone; Axis 2 is attached to the cutting tool model and is located at the center of the end face circle of the milling cutter. Through the control of the program:
① The gear blank rotary shaft is inclined to the horizontal plane by one δ B angle – 24.85 °;
② The cone apex of the base cone, axis1, is located on the rotation axis of the c axis;
③ Axis1 and Axis2 are located in the same horizontal plane, and the coordinate values are equal in the X direction, and the distance in the Y direction is the R value of the blade radius.
This is the initial position state of milling the concave tooth surface of spiral bevel gear, as shown in the figure.
Combined with the displacement expression of the gear blank along the x-axis direction obtained from the analysis of gear cutting motion – the coordinate value of the x-axis at the initial position of the formula, the displacement expression of the gear blank in the x-axis direction in the milling simulation process of spiral bevel gear can be obtained:
Where: R – blade radius, size 149.07; ω 2 — rotation speed of gear blank around axis C.
Since the angle difference of C axis between two adjacent steps of the NC program is 0.1 °, the angle difference in the formula is ω 2=0.1。 Based on the above analysis, the coordinate points of the gear blank in the x-axis direction are calculated and collected by using MATLAB and Excel software. The matlab function for solving the coordinate value of the tooth blank moving along the x-axis direction in the process of milling the concave tooth surface of spiral bevel gear is as follows:

Through the operation of the above matlab functions, the position coordinate points of the gear blank on the x-axis during gear cutting can be listed in column F of Excel table Sheet1 with the file name of “Youxuan aomian”. Due to a-axis rotation ω 1 and c-axis rotation ω 2 are rotating at a uniform speed. According to the analysis in this section, the coordinate values of axis A and axis C are listed in column B and column D of the same excel table in the form of equal difference sequence. Then enter the names of each coordinate axis – A, C and X – in columns a, C and e of Sheet1 in Excel table. Next, copy and paste the contents in the excel table into the notepad file. So far, the main part of the NC program in the cutting process of concave tooth surface has been prepared. Finally, the NC program of concave tooth surface can be completed by adding NC program header, initial feed position program, cycle and indexing statements. Using the same method, the NC machining program of convex tooth surface of spiral bevel gear is compiled.