Abstract
This paper addresses the reliability optimization design of helical gear wear under data scarcity conditions. A non-probabilistic interval model is employed to characterize the uncertainties in parameters. Leveraging Hertz contact theory and Archard wear theory, a reliability optimization design method is proposed for helical gear. Initially, a finite element analysis (FEA) model is developed to analyze the contact stresses and wear patterns on the tooth surfaces during gear meshing. Considering uncertainties in gear geometry, material properties, and load conditions, a reliability optimization model is established with non-probabilistic reliability indices constraints related to contact strength and wear amount. The results demonstrate that under the constraints of non-probabilistic reliability indices, the gear pair’s volume is reduced by 25.11%, and the wear is decreased by 16.09%, verifying the effectiveness of the proposed method.
1. Introduction
Helical gear is widely used in various industries such as aerospace, shipping, automotive, and precision instruments due to their high transmission efficiency, long service life, reliable operation, and stable transmission ratio [1-2]. However, during the meshing process, gear wear can lead to noise, vibration, reduced transmission efficiency, and even premature failure, significantly impacting the safe operation of the transmission system. The uncertainties in gear geometry, material properties, and load conditions contribute to the unpredictability of gear wear, necessitating a comprehensive reliability analysis that accounts for these uncertainties.
Traditional probability-based reliability analysis methods require substantial experimental data to determine the probability distribution of variables. However, due to data scarcity, establishing accurate probability distribution models becomes challenging, rendering traditional methods inapplicable. Consequently, researchers have turned to non-probabilistic models, particularly interval models, which only require the upper and lower bounds of uncertain parameters [3-4].
Gear wear is influenced by multiple factors such as temperature, lubrication, load, and material properties, resulting in a complex wear mechanism. Archard’s simplified wear model is commonly used for gear wear analysis [5]. Researchers have extended this model to analyze the wear distribution on spur and helical gear by discretizing the tooth profiles into finite points [6-8]. Nonetheless, studies focusing on the impact of uncertainties in gear geometry, material properties, and load conditions on wear are relatively scarce.
This paper proposes a non-probabilistic reliability analysis and optimization design method for helical gear wear under data scarcity. The uncertainties in gear geometry, material properties, and load conditions are considered, and reliability indices related to contact strength and wear amount are established as constraints for optimization. The optimized design achieves a more reliable and economical gear configuration.
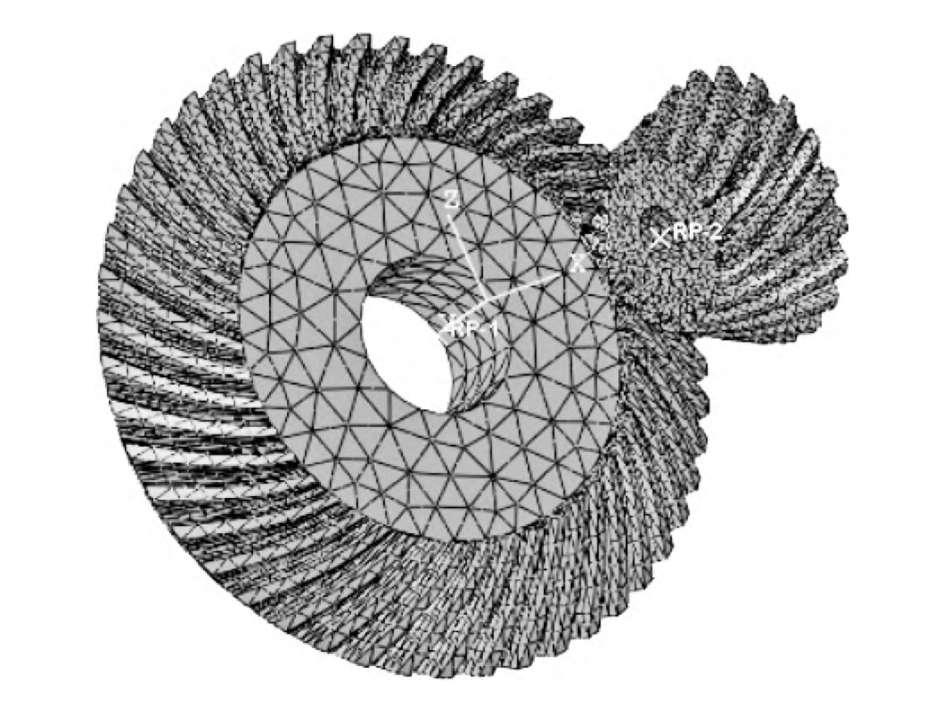
2. Geometric Modeling of Helical Gear Pair
The geometric shape of a helical gear directly influences the contact conditions and motion transmission during meshing, significantly affecting tooth surface wear. Therefore, precise geometric modeling is essential. The geometry of a standard involute helical gear is determined by seven basic parameters: number of teeth (z), normal module (mn), tooth width (B), normal pressure angle (α), normal addendum coefficient (ha), normal clearance coefficient (c), and helix angle (β). For gears with modification, the normal modification coefficient (x) is also considered.
Using UG NX software combined with secondary development techniques, a parameterized 3D model of the helical gear is established by defining key geometric parameters and relationships through expressions.
For meshing analysis, a gear pair model is constructed by assembling the drive and driven gears in a single file using different coordinate systems to avoid interference and ensure accurate meshing positions.
3. Finite Element Analysis of Helical Gear Wear
The materials of both the drive and driven gears are 20CrMnTi, with properties listed in Table 1. A fine mesh is applied to the tooth contact areas, while coarser meshes are used for the hub and root regions to reduce computational costs. The contact between tooth surfaces is controlled using a penalty function with a friction coefficient of 0.1.
The loading process is divided into three steps:
- Apply a small angular displacement to the drive gear to initiate contact.
- Restrict the drive gear’s degrees of freedom and apply a resisting torque (T = 3.0 × 10^5 N·mm) to the driven gear.
- Maintain the torque on the driven gear and rotate the drive gear at a speed of 140 rpm to simulate meshing.
The contact stresses during gear meshing are analyzed, and the maximum contact stress (δmax) is identified. The von Mises stress distributions at different meshing stages.
A user-defined material subroutine (UMAT) is implemented in ABAQUS to analyze wear depth using the ALE (Arbitrary Lagrangian-Eulerian) adaptive meshing technique. The wear depth distributions along the action line for different tooth surfaces are presented.
4. Non-Probabilistic Reliability Analysis Based on Interval Model
Uncertainty variables are selected from three aspects: gear geometry (e.g., mn, β, B, z), material properties (e.g., E, ν), and load conditions (e.g., n, T). The interval settings for these variables are shown in Table 2.
Two failure modes are considered: contact strength failure and wear damage. The corresponding functional functions are defined as:
- Contact strength functional: g1(x) = δHS – δmax(x)
- Wear damage functional: g2(x) = Ws – Wh(x)
where δHS and Ws are the allowable contact stress and wear depth, respectively.
Due to the complex nonlinear relationships between the responses and input variables, a Kriging approximation model is employed to fit the response surfaces.
The non-probabilistic reliability indices (η1 for contact strength and η2 for wear) are calculated using optimization methods. Results indicate that both reliability indices are greater than 1, confirming the structural reliability of the gear pair.
5. Reliability Optimization Design
An optimization model is formulated with the objective of minimizing the total gear pair volume (V) while ensuring that both reliability indices (η1 and η2) are greater than 1. The optimization framework involves nested loops: an inner loop for reliability index calculation using sequential quadratic programming and an outer loop for design variable optimization using a genetic algorithm.
The optimized design variables and corresponding gear pair volume are presented in Table 3.
After rounding off the optimal design variables, the gear pair volume is reduced by 25.11%, and the maximum wear depth is decreased by 16.09%, validating the effectiveness of the proposed method.
6. Conclusion
This paper presents a non-probabilistic reliability analysis and optimization design method for helical gear wear under data scarcity. By considering uncertainties in gear geometry, material properties, and load conditions, non-probabilistic reliability indices related to contact strength and wear amount are established. An optimization model is formulated to minimize the gear pair volume while ensuring structural reliability. The optimized design results in a 25.11% volume reduction and a 16.09% decrease in wear depth, demonstrating the effectiveness of the proposed method.
