Abstract: This article focuses on the dynamic characteristics of spur gears with multiple faults, considering the tooth root transition curve. It first introduces the background and significance of studying spur gear faults. Then, it presents a detailed analysis of the gear pair coupling vibration analysis model and the calculation method of gear time-varying meshing stiffness considering the tooth root transition curve. The article also includes gear dynamics simulation and test response analysis for different faults such as cracks, pitting, and missing teeth. The results show that the proposed method can accurately calculate the meshing stiffness and the dynamic responses of gears with different faults, which are consistent with the experimental results. This research provides a valuable reference for the fault diagnosis and dynamic analysis of spur gear systems.

1. Introduction
Spur gear systems are widely used in various mechanical equipment. During operation, faults such as cracks, pitting, and missing teeth may occur due to factors like alternating single and double tooth meshing, which can affect the performance and reliability of the gear system. Therefore, studying the dynamics of spur gears with faults is of great significance for understanding the fault mechanism and performing fault diagnosis.
The meshing stiffness of gears, which varies with time during operation, is a major dynamic excitation for gear system vibration. Many scholars have conducted extensive research on stiffness calculation and vibration characteristic analysis. For example, in 1987, YANG D C H et al. proposed the energy method to calculate the time-varying meshing stiffness of gear pairs. In 2004, TIAN X H improved this model by considering the influence of shear potential energy on meshing stiffness. SAINSOT proposed a formula for calculating the deformation of the gear matrix, and CHAARI F et al. incorporated the stiffness change caused by the gear matrix deformation into the calculation of gear meshing stiffness and analyzed the effects of gear spalling or tooth breakage on meshing stiffness. However, previous studies often simplified the tooth root transition curve. In recent years, domestic scholars have continuously improved the calculation method of meshing stiffness to make it more accurate and in line with the actual situation.
This article aims to comprehensively consider factors such as tooth deformation, gear matrix deformation, and contact deformation, and use a more realistic tooth root transition curve to accurately and efficiently calculate the time-varying meshing stiffness of gears. By establishing a parallel gear pair dynamics equation using the lumped parameter method and analyzing the effects of multiple faults on the time-varying meshing stiffness, the dynamic responses caused by different gear faults are simulated and compared with experimental results to analyze the vibration characteristics of gears with different faults.
2. Gear Pair Coupling Vibration Analysis Model
In the case of considering tooth surface friction, a meshing coupling type dynamics model of a parallel gear pair is established. The corresponding dynamic equations are:
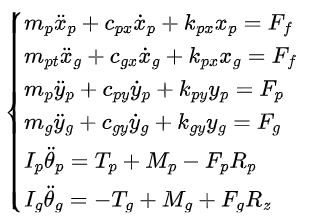

By solving these equations, the dynamic responses of the parallel gear pair coupling vibration can be obtained.
3. Gear Time-Varying Meshing Stiffness Considering Tooth Root Transition Curve
The internal excitation during the operation of a parallel gear pair mainly comes from the dynamic stiffness excitation between teeth. The energy method is a relatively accurate method for calculating the gear time-varying meshing stiffness. In a parallel gear pair, each tooth is assumed to be a cantilever beam with a variable cross-section, and the meshing stiffness of a tooth can be expressed as the ratio of the normal force on the tooth surface to the deformation at the point of force application on the tooth. The deformation at the point of meshing force application on the tooth is considered to be generated by three main parts:




When a gear has a missing tooth fault, the double-tooth meshing area at the missing tooth part will become a single tooth, and the single-tooth meshing area will become toothless. The corresponding meshing stiffness will also change. To calculate the time-varying meshing stiffness of a gear with a missing tooth fault, it is only necessary to subtract the influence of a single tooth on the meshing stiffness calculation during the meshing stiffness calculation process.
4. Gear Dynamics Simulation and Test Response Analysis
To analyze the fault dynamics responses of a parallel gear pair, the parallel gearbox of the test bench is taken as the object. The main parameters are shown in Table 1. The pinion is the driving wheel, and the simulation of the driving wheel speed is 1800 r/min, with a meshing frequency of 690 Hz. The support stiffness and support damping in the simulation model are identified by the model correction method, which are km=kss=2.77✖10^5N/m, kw=kw=5.71✖10^6N/m, Cps=Cps=3.02✖10^3N•s/m, cpy=cw=5.38X10^3N•s/m. The radial vibration data is collected with a sampling frequency of 51200 Hz to compare the dynamic responses of the simulation and test gearboxes in different states.
| Parameter | Driving Wheel | Driven Wheel |
|---|---|---|
| Number of Teeth | 23 | 84 |
| Module (mm) | 2 | 2 |
| Pressure Angle () | 20 | 20 |
| Tooth Width (mm) | 20 | 20 |
| Mass (kg) | 0.22 | 1.9 |
| Moment of Inertia () | ||
| Rotational Speed (r/min) | 1800 | 493 |
4.1 Crack Fault Simulation and Test Response Analysis
For the crack fault test piece, the crack angle at the midpoint of the tooth root transition line, and the crack depth . The crack parameters simulated are consistent with those of the test piece. The simulation and test dynamic responses of the crack gear. From the time-domain signal, it can be seen that there are impacts in each period. In the frequency spectrum, the amplitude of the frequency components related to the shaft speed is obvious, the energy near the second harmonic of the meshing frequency is relatively concentrated, and there are also side lobe signals modulated by the shaft speed.
4.2 Pitting Fault Simulation and Test Response Analysis
For the pitting fault test piece, the length, width, and height of the surface pitting at the indexing position are αs=1mm, Ws=10mm, hs=0.5mm respectively. The pitting parameters simulated are consistent with those of the test piece. In the pitting gear simulation test, due to the small pits on the surface of the pitting gear, the test process response is not obvious. From the time-domain signals, it can be seen that there are slight vibration amplitude jumps in each period, indicating that the gear meshing impact is small and gentle. In the frequency spectrum, the side lobe amplitudes of the shaft speed and meshing frequency are small and concentrated, and the meshing frequency and its higher harmonics are still the main frequency components.
4.3 Missing Tooth Fault Simulation and Test Response Analysis
For the missing tooth fault gear test piece. Due to the large influence of the missing tooth on the gear meshing process, an obvious impact sound can be heard during the test. In the dynamic responses of the missing tooth gear, whether in the simulation or test time-domain signals, it can be seen that there are very large impacts in each period. Affected by short pulses, in the frequency spectrum, the number of side lobes of the meshing frequency is large, the range is wide, and the amplitude is large, and the meshing frequency and its higher harmonics are easily submerged in these side lobe signals.
5. Conclusion
- Considering the tooth root transition curve enables more accurate calculation of gear meshing stiffness. The fault characteristics reflected by the dynamic responses of gears with multiple faults such as cracks, pitting, and missing teeth are consistent with the experimental results.
- The proposed method can simulate the response characteristics of the same faulty gear at different fault degrees, which can provide reference for the establishment of a subsequent parallel gear system fault database.
- The fault characteristics of slight pitting faults are not obvious in the frequency domain response and are similar to the frequency components and distribution of normal gears, which requires further research.
In summary, this research on the dynamic characteristics of spur gears with multiple faults considering the tooth root transition curve has made significant progress. It not only provides a more accurate method for calculating gear meshing stiffness but also verifies the effectiveness of this method through simulation and experimental comparisons. The consistency between the simulation results and the experimental results for different fault types indicates that this method has strong practical application value.
For future research, more attention can be paid to improving the accuracy of fault simulation for slight pitting faults. This may involve exploring more detailed models of pitting formation and its influence on gear dynamics. Additionally, further investigations can be carried out to study the long-term effects of multiple faults on gear performance and reliability. This could include analyzing the degradation of gear meshing stiffness over time and its impact on the overall gear system operation.
Moreover, the research can be extended to consider other factors that may affect gear dynamics, such as lubrication conditions, temperature variations, and manufacturing tolerances. Understanding how these factors interact with gear faults can provide a more comprehensive understanding of gear system behavior and lead to more effective fault diagnosis and preventive maintenance strategies.
In conclusion, the study of spur gear faults considering the tooth root transition curve is an important area of research that has the potential to improve the reliability and performance of gear systems in various industrial applications. Continued research in this field will contribute to the development of more advanced gear fault diagnosis techniques and the optimization of gear system design and operation.
