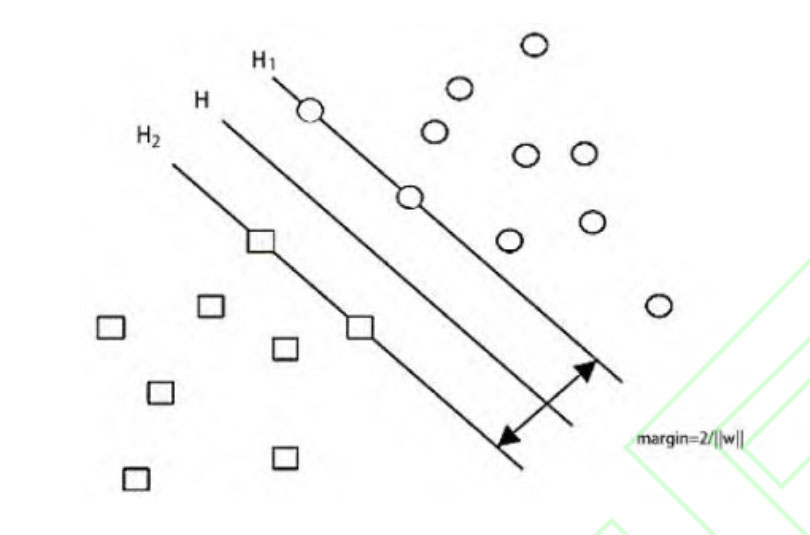
The rotation direction of helical gears is classified using SVM support vector machine, which is a commonly used classification algorithm in machine learning. It can rely on divided data to analyze its unknown categories and obtain their respective categories. The process of solving a given problem is to search for an action sequence for a given classification target state and transform it from a real-time state to a target state. SVM is mainly used to classify objects into two types, which can also be multiple types. For a variable with n features, X=(X1, X2,…, Xn) T, which is represented as:
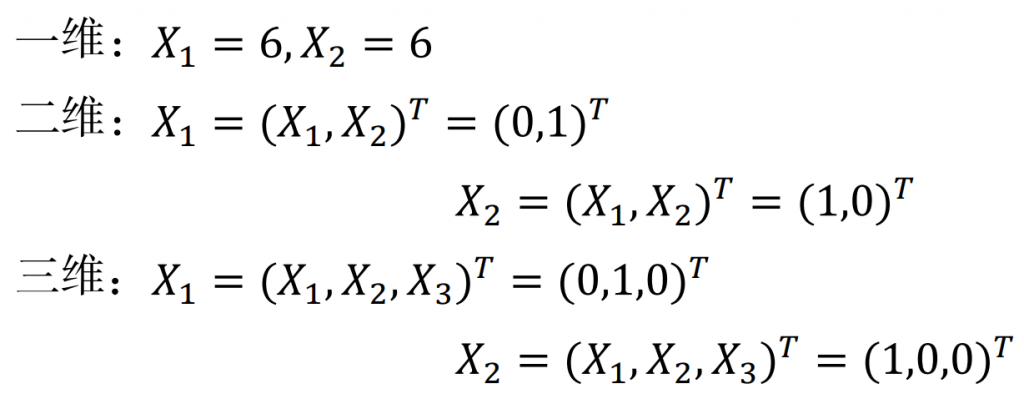
In the SVM developed from the linear separable optimal classification, consider making the points of the training set as far away from the classification plane as possible in a hyperplane, so as to maximize the margin of the blank area on both sides of the classification plane.

Compared to other commonly used machine vision classification algorithms, such as BP neural network and template matching based classification algorithms, SVM classifiers can also perform well in small sample training sets. Initially, SVM algorithms were proposed for binary classification problems, so SVM algorithms were used for gear rotation classification.
SVM detection algorithm steps
- Classify the dataset
- Traverse the dataset and resize the image
- Dataset training
- Adjust important parameters of SVM
- Read the grayscale area of the image to be classified
- Perform SVM classification
- Display classification results
To train an SVM classifier, the first step is to prepare an image dataset of the left and right rotation of the helical gear. The images of the left and right rotation of the helical gear are binarized to extract their feature parameters. Then, the processed images are labeled and added to the SVM classifier to begin learning. The algorithm steps are shown in Table 1.
| Rotation direction | Sinistral rotation | Dextral rotation | Number |
| Data Set | 35 | 35 | 70 |
| Test Set | 20 | 20 | 40 |
When dealing with linearly indivisible problems, SVM transforms them into higher dimensions to achieve classification, and using kernel functions can avoid the computational complexity that increases sharply due to dimension transformation. The commonly used kernel functions include Linear, PH, PHI, and RBF. Choosing an appropriate kernel function plays a crucial role in the accuracy of classification. To verify the selection of the optimal kernel function, a total of 110 data samples were selected. The samples of the dataset are shown in Table 2. The classification accuracy of each kernel function is shown in Table 3.
| Kernel function | Linear | PH | PIH | RBF |
| Accuracy | 95% | 93% | 93.5% | 98% |
